| (50 intermediate revisions by 10 users not shown) | |||
| Line 1: | Line 1: | ||
| − | ''' | + | <center><font size= 4> |
| + | '''[[ECE662]]: Statistical Pattern Recognition and Decision Making Processes''' | ||
| + | </font size> | ||
| + | |||
| + | Spring 2008, [[user:mboutin|Prof. Boutin]] | ||
| + | |||
| + | [[Slectures|Slecture]] | ||
| + | |||
| + | <font size= 3> Collectively created by the students in [[ECE662:BoutinSpring08_OldKiwi|the class]]</font size> | ||
| + | </center> | ||
| + | |||
| + | ---- | ||
| + | =Lecture 23 Lecture notes= | ||
| + | Jump to: [[ECE662_Pattern_Recognition_Decision_Making_Processes_Spring2008_sLecture_collective|Outline]]| | ||
| + | [[Lecture 1 - Introduction_OldKiwi|1]]| | ||
| + | [[Lecture 2 - Decision Hypersurfaces_OldKiwi|2]]| | ||
| + | [[Lecture 3 - Bayes classification_OldKiwi|3]]| | ||
| + | [[Lecture 4 - Bayes Classification_OldKiwi|4]]| | ||
| + | [[Lecture 5 - Discriminant Functions_OldKiwi|5]]| | ||
| + | [[Lecture 6 - Discriminant Functions_OldKiwi|6]]| | ||
| + | [[Lecture 7 - MLE and BPE_OldKiwi|7]]| | ||
| + | [[Lecture 8 - MLE, BPE and Linear Discriminant Functions_OldKiwi|8]]| | ||
| + | [[Lecture 9 - Linear Discriminant Functions_OldKiwi|9]]| | ||
| + | [[Lecture 10 - Batch Perceptron and Fisher Linear Discriminant_OldKiwi|10]]| | ||
| + | [[Lecture 11 - Fischer's Linear Discriminant again_OldKiwi|11]]| | ||
| + | [[Lecture 12 - Support Vector Machine and Quadratic Optimization Problem_OldKiwi|12]]| | ||
| + | [[Lecture 13 - Kernel function for SVMs and ANNs introduction_OldKiwi|13]]| | ||
| + | [[Lecture 14 - ANNs, Non-parametric Density Estimation (Parzen Window)_OldKiwi|14]]| | ||
| + | [[Lecture 15 - Parzen Window Method_OldKiwi|15]]| | ||
| + | [[Lecture 16 - Parzen Window Method and K-nearest Neighbor Density Estimate_OldKiwi|16]]| | ||
| + | [[Lecture 17 - Nearest Neighbors Clarification Rule and Metrics_OldKiwi|17]]| | ||
| + | [[Lecture 18 - Nearest Neighbors Clarification Rule and Metrics(Continued)_OldKiwi|18]]| | ||
| + | [[Lecture 19 - Nearest Neighbor Error Rates_OldKiwi|19]]| | ||
| + | [[Lecture 20 - Density Estimation using Series Expansion and Decision Trees_OldKiwi|20]]| | ||
| + | [[Lecture 21 - Decision Trees(Continued)_OldKiwi|21]]| | ||
| + | [[Lecture 22 - Decision Trees and Clustering_OldKiwi|22]]| | ||
| + | [[Lecture 23 - Spanning Trees_OldKiwi|23]]| | ||
| + | [[Lecture 24 - Clustering and Hierarchical Clustering_OldKiwi|24]]| | ||
| + | [[Lecture 25 - Clustering Algorithms_OldKiwi|25]]| | ||
| + | [[Lecture 26 - Statistical Clustering Methods_OldKiwi|26]]| | ||
| + | [[Lecture 27 - Clustering by finding valleys of densities_OldKiwi|27]]| | ||
| + | [[Lecture 28 - Final lecture_OldKiwi|28]] | ||
| + | ---- | ||
| + | ---- | ||
| + | ==Clustering Method, given the pairwise distances== | ||
| + | |||
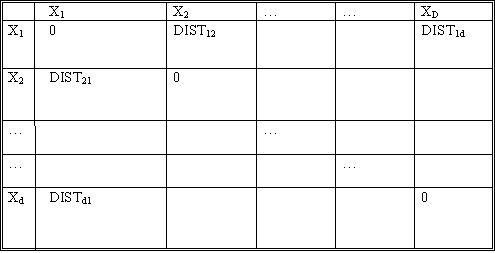
| + | Let d be the number of objects. Let <math>DIST_{ij}</math> denote the distance between objects <math>X_i</math> and <math>X_j</math>. The notion of distance here is not clear unless the application itself is considered. For example, when dealing with some psychological studies data, we may have to consult the psychologist himself as to what is the "distance" between given two concepts. These distances form the input to our clustering algorithm. | ||
| + | |||
| + | The constraint on these distances is that they be | ||
| + | |||
| + | - symmetric between any two objects (<math>DIST_{ij}=DIST_{ji}</math>) | ||
| + | |||
| + | - always positive (<math>DIST_{ij}>=0</math>) | ||
| + | |||
| + | - zero for distance of an object from itself (<math>DIST_{ii}=0</math>) | ||
| + | |||
| + | - follow <math>\bigtriangleup</math> inequality | ||
| + | |||
| + | [[Image:Dist_table_OldKiwi.jpg]] Table 1 | ||
| + | |||
| + | ''Idea:'' | ||
| + | |||
| + | If <math>DIST_{ij}</math> small => <math>X_i</math>, <math>X_j</math> in same cluster. | ||
| + | |||
| + | If <math>DIST_{ij}</math> large => <math>X_i</math>, <math>X_j</math> in different clusters. | ||
| + | |||
| + | *How to define small or large? One option is to fix a threshold <math>t_0</math>. | ||
| + | |||
| + | such that | ||
| + | |||
| + | <math>t_0</math> < "typical" distance between clusters, and | ||
| + | |||
| + | <math>t_0</math> > "typical" distance within clusters. | ||
| + | |||
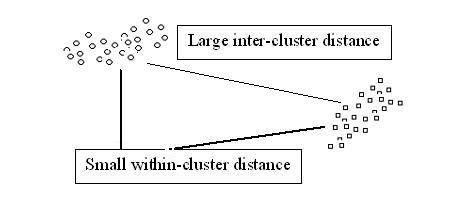
| + | Consider the following situation of objects distribution. This is a very conducive situation, and almost any clustering method will work well. | ||
| + | |||
| + | [[Image:ideal_situation_OldKiwi.jpg]] Figure 1 | ||
| + | |||
| + | |||
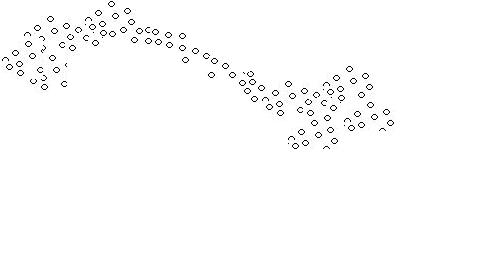
| + | A problem arises when thew following situation arises: | ||
| + | |||
| + | [[Image:elongated_cluster_OldKiwi.jpg]] Figure 2 | ||
| + | |||
| + | Although we see two separate clusters with a thin distribution of objects in between, the algorithm mentioned above identifies only one cluster. | ||
| + | |||
| + | |||
| + | ==Graph Theory Clustering== | ||
dataset <math>\{x_1, x_2, \dots , x_d\}</math> no feature vector given. | dataset <math>\{x_1, x_2, \dots , x_d\}</math> no feature vector given. | ||
| Line 13: | Line 99: | ||
Definitions: | Definitions: | ||
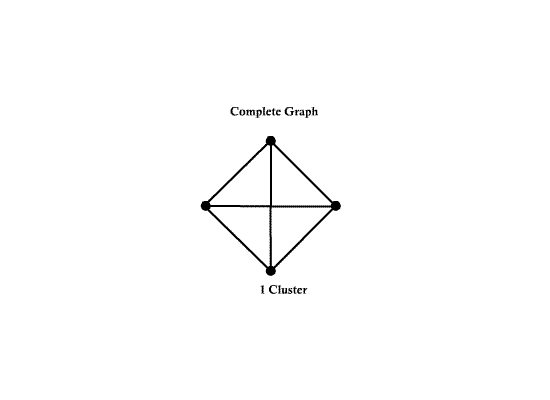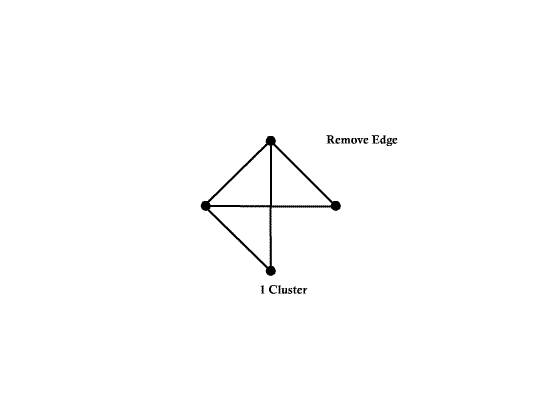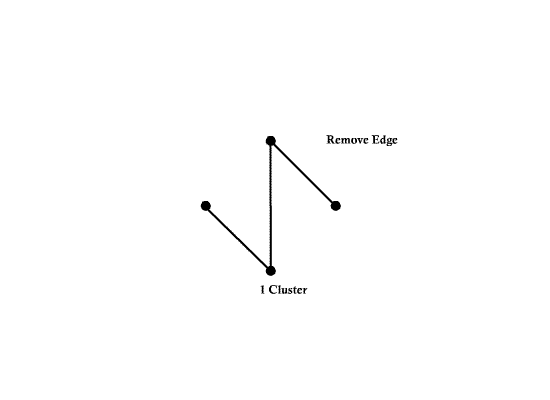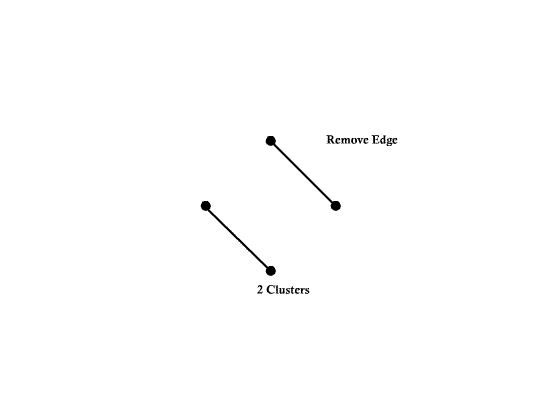
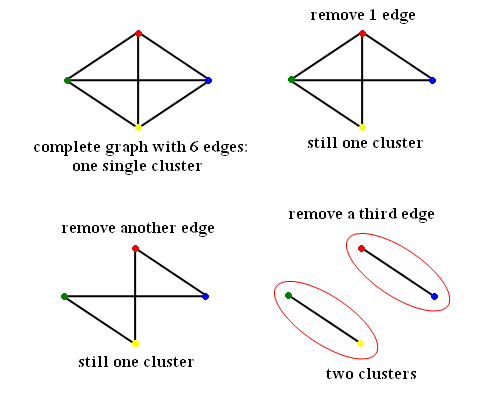
| − | * A ''complete graph'' is a graph with d(d-1)/2 edges. | + | * A ''complete graph'' is a graph with <math>d(d-1)/2</math> edges. |
| − | + | Example: | |
| + | Number of nodes d = 4 | ||
| + | Number of edges e = 6 | ||
| + | [[Image:ECE662_lect23_OldKiwi.gif]] Figure 3 | ||
| − | * A ''path'' in a graph between | + | [[Image:Kiwi_lec_edges_figure_OldKiwi.PNG]] Figure 4 |
| + | |||
| + | * A ''subgraph'' <math>G'</math> of a graph <math>G=(V,E,f)</math> is a graph <math>(V',E',f')</math> such that <math>V'\subset V</math> <math>E'\subset E</math> <math>f'\subset f</math> restricted to <math>E'</math> | ||
| + | |||
| + | * A ''path'' in a graph between <math>V_i,V_k \subset V_k</math> is an alternating sequence of vertices and edges containing no repeated edges and no repeated vertices and for which <math>e_i</math> is incident to <math>V_i</math> and <math>V_{i+1}</math>, for each <math>i=1,2,\dots,k-1</math>. (<math>V_1 e_1 V_2 e_2 V_3 \dots V_{k-1} e_{k-1} V_k</math>) | ||
* A graph is "''connected''" if a path exists between any two vertices in the graph | * A graph is "''connected''" if a path exists between any two vertices in the graph | ||
| Line 23: | Line 116: | ||
* A ''component'' is a maximal connected graph. (i.e. includes as many nodes as possible) | * A ''component'' is a maximal connected graph. (i.e. includes as many nodes as possible) | ||
| − | * A ''maximal complete subgraph'' of a graph G is a complete subgraph of G that is not a proper subgraph of any other complete subgraph of G. | + | * A ''maximal complete subgraph'' of a graph <math>G</math> is a complete subgraph of <math>G</math> that is not a proper subgraph of any other complete subgraph of <math>G</math>. |
| − | * A ''cycle'' is a path of non-trivial length k that comes back to the node where it started | + | * A ''cycle'' is a path of non-trivial length <math>k</math> that comes back to the node where it started |
* A ''tree'' is a connected graph with no cycles. The weight of a tree is the sum of all edge weights in the tree. | * A ''tree'' is a connected graph with no cycles. The weight of a tree is the sum of all edge weights in the tree. | ||
| Line 31: | Line 124: | ||
* A ''spanning tree'' is a tree containing all vertices of a graph. | * A ''spanning tree'' is a tree containing all vertices of a graph. | ||
| − | * A ''minimum spanning tree'' (MST) of a graph G is tree having minimal weight among all spanning trees of G. | + | * A ''minimum spanning tree'' (MST) of a graph G is tree having minimal weight among all spanning trees of <math>G</math>. |
| + | |||
| + | |||
| + | (There are more terminologies for graph theory [http://en.wikipedia.org/wiki/Glossary_of_graph_theory here] ) | ||
| + | |||
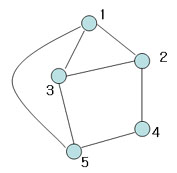
| + | Illustration [[Image:Spark1_OldKiwi.jpg]] Figure 5 | ||
| + | |||
| + | |||
| + | [[Image:Spark2_OldKiwi.jpg]] Figure 6 | ||
| + | This is spanning tree (MST with weight 4) | ||
| + | |||
| + | [[Image:Spark3_OldKiwi.jpg]] Figure 7 | ||
| + | Another spanning tree (Also, MST with weight 4) | ||
| + | |||
| + | [[Image:Spark4_OldKiwi.jpg]] Figure 8 | ||
| + | Not spannning tree (Include 'cycle') | ||
| + | |||
| + | [[Image:Spark5_OldKiwi.jpg]] Figure 9 | ||
| + | Not spanning tree (No edge for 4) | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
| + | ==Graphical Clustering Methods== | ||
| + | |||
| + | * "Similarity Graph Methods" | ||
| + | |||
| + | Choose distance threshold <math>t_0</math> | ||
| + | |||
| + | If <math>dis(X_i,X_j)<t_0</math> draw an ege between <math>X_i</math> and <math>X_j</math> | ||
| + | |||
| + | |||
| + | |||
| + | Example) <math>t_0= 1.3</math> | ||
| + | |||
| + | [[Image:Fig2_1_OldKiwi.jpg]] | ||
| + | Fig 3-1 | ||
| + | |||
| + | Can define clusters as the connected component of the similarity graph | ||
| + | |||
| + | => Same result as "Single linkage algorithms" | ||
| + | |||
| + | <math>X_i \sim X_j</math> if there is chain | ||
| + | |||
| + | <math>X_i \sim X_{i_1} \sim X_{i_2} \sim \cdots X_{i_k} \sim X_{j}</math> complete | ||
| + | |||
| + | Can also define clusters as the maximal subgraphs of similarity graph | ||
| + | |||
| + | [[Image:Fig2_2_OldKiwi.jpg]] | ||
| + | Fig 3-2 | ||
| + | |||
| + | =>this yeilds more compact, less enlongated clusters | ||
| + | |||
| + | The approach above is not good for, say, | ||
| + | |||
| + | [[Image:Fig3_3_OldKiwi.jpg]] | ||
| + | Fig 3-3 | ||
| + | ---- | ||
| + | Previous: [[Lecture_22_-_Decision_Trees_and_Clustering_OldKiwi|Lecture 22]] | ||
| + | Next: [[Lecture_24_-_Clustering_and_Hierarchical_Clustering_OldKiwi|Lecture 24]] | ||
| + | |||
| + | [[ECE662:BoutinSpring08_OldKiwi|Back to ECE662 Spring 2008 Prof. Boutin]] | ||
| + | [[Category:ECE662]] | ||
| + | [[Category:decision theory]] | ||
| + | [[Category:lecture notes]] | ||
| + | [[Category:pattern recognition]] | ||
| + | [[Category:slecture]] | ||
Latest revision as of 10:23, 10 June 2013
ECE662: Statistical Pattern Recognition and Decision Making Processes
Spring 2008, Prof. Boutin
Collectively created by the students in the class
Contents
Lecture 23 Lecture notes
Jump to: Outline| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| 20| 21| 22| 23| 24| 25| 26| 27| 28
Clustering Method, given the pairwise distances
Let d be the number of objects. Let $ DIST_{ij} $ denote the distance between objects $ X_i $ and $ X_j $. The notion of distance here is not clear unless the application itself is considered. For example, when dealing with some psychological studies data, we may have to consult the psychologist himself as to what is the "distance" between given two concepts. These distances form the input to our clustering algorithm.
The constraint on these distances is that they be
- symmetric between any two objects ($ DIST_{ij}=DIST_{ji} $)
- always positive ($ DIST_{ij}>=0 $)
- zero for distance of an object from itself ($ DIST_{ii}=0 $)
- follow $ \bigtriangleup $ inequality
Idea:
If $ DIST_{ij} $ small => $ X_i $, $ X_j $ in same cluster.
If $ DIST_{ij} $ large => $ X_i $, $ X_j $ in different clusters.
- How to define small or large? One option is to fix a threshold $ t_0 $.
such that
$ t_0 $ < "typical" distance between clusters, and
$ t_0 $ > "typical" distance within clusters.
Consider the following situation of objects distribution. This is a very conducive situation, and almost any clustering method will work well.
A problem arises when thew following situation arises:
Although we see two separate clusters with a thin distribution of objects in between, the algorithm mentioned above identifies only one cluster.
Graph Theory Clustering
dataset $ \{x_1, x_2, \dots , x_d\} $ no feature vector given.
given $ dist(x_i , x_j) $
Construct a graph:
- node represents the objects.
- edges are relations between objects.
- edge weights represents distances.
Definitions:
- A complete graph is a graph with $ d(d-1)/2 $ edges.
Example:
Number of nodes d = 4 Number of edges e = 6
- A subgraph $ G' $ of a graph $ G=(V,E,f) $ is a graph $ (V',E',f') $ such that $ V'\subset V $ $ E'\subset E $ $ f'\subset f $ restricted to $ E' $
- A path in a graph between $ V_i,V_k \subset V_k $ is an alternating sequence of vertices and edges containing no repeated edges and no repeated vertices and for which $ e_i $ is incident to $ V_i $ and $ V_{i+1} $, for each $ i=1,2,\dots,k-1 $. ($ V_1 e_1 V_2 e_2 V_3 \dots V_{k-1} e_{k-1} V_k $)
- A graph is "connected" if a path exists between any two vertices in the graph
- A component is a maximal connected graph. (i.e. includes as many nodes as possible)
- A maximal complete subgraph of a graph $ G $ is a complete subgraph of $ G $ that is not a proper subgraph of any other complete subgraph of $ G $.
- A cycle is a path of non-trivial length $ k $ that comes back to the node where it started
- A tree is a connected graph with no cycles. The weight of a tree is the sum of all edge weights in the tree.
- A spanning tree is a tree containing all vertices of a graph.
- A minimum spanning tree (MST) of a graph G is tree having minimal weight among all spanning trees of $ G $.
(There are more terminologies for graph theory here )
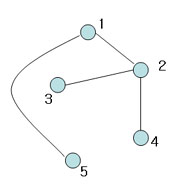 Figure 6
This is spanning tree (MST with weight 4)
Figure 6
This is spanning tree (MST with weight 4)
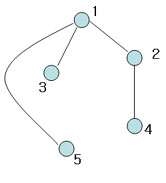 Figure 7
Another spanning tree (Also, MST with weight 4)
Figure 7
Another spanning tree (Also, MST with weight 4)
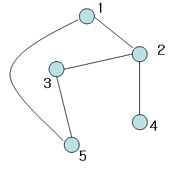 Figure 8
Not spannning tree (Include 'cycle')
Figure 8
Not spannning tree (Include 'cycle')
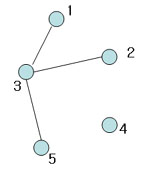 Figure 9
Not spanning tree (No edge for 4)
Figure 9
Not spanning tree (No edge for 4)
Graphical Clustering Methods
- "Similarity Graph Methods"
Choose distance threshold $ t_0 $
If $ dis(X_i,X_j)<t_0 $ draw an ege between $ X_i $ and $ X_j $
Example) $ t_0= 1.3 $
Fig 3-1
Can define clusters as the connected component of the similarity graph
=> Same result as "Single linkage algorithms"
$ X_i \sim X_j $ if there is chain
$ X_i \sim X_{i_1} \sim X_{i_2} \sim \cdots X_{i_k} \sim X_{j} $ complete
Can also define clusters as the maximal subgraphs of similarity graph
Fig 3-2
=>this yeilds more compact, less enlongated clusters
The approach above is not good for, say,
Fig 3-3
Previous: Lecture 22 Next: Lecture 24