Lecture 18 Lecture notes

Jump to: Outline| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| 20| 21| 22| 23| 24| 25| 26| 27| 28

Nearest Neighbors Classification Rule (Alternative Approach)

• Find invariant coordinates

$ \varphi : \Re ^k \rightarrow \Re ^n $ such that $ \varphi (x) = \varphi (\bar x) $ for all $ x, \bar x $ which are related by a rotation & translation Do NOT trivialize!

Example: $ \varphi (x) =0 $ gives us a trivial invariant coordinate. But, you lose information about separation, since everything is mapped to zero.

Want $ \varphi (x) = \varphi (\bar x) $ $ \Leftrightarrow x, \bar x $ are related by a rotation and translation

Example: $ p=(p_1,p_2,\cdots, p_N) \in \Re ^{3 \times N} $ $ \varphi $ maps representation position of tags on body onto $ (d_{12},d_{13},d_{14},\cdots , d_{N-1, N} ) $ where $ d_{ij} $= Euclidean distance between $ p_i $ and $ p_j $

In the above example, we can reconstruct up to a rotation and translation.

WARNING: Euclidean distance in the invariant coordinate space has nothing to do with Euclidean distance or Procrustes distance in initial feature space.

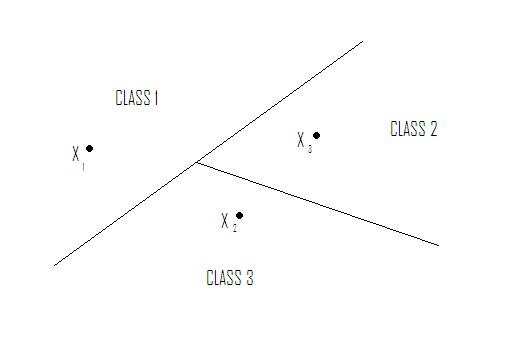
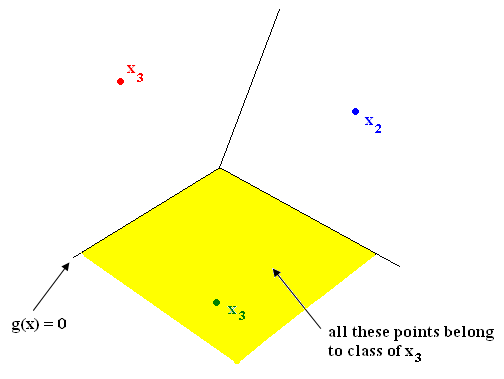
Nearest Neighbor in $ \Re ^2 $ yields tessellation (tiling of floor with 2D shapes such that 1) no holes and 2) cover all of $ \Re ^2 $ ). The tessellations separate sample space into regions. Shape of cells depends on metric chosen. See Figure 1.

Figure 1 - Separation of Sample Space using Tessellations

Figure 1b - Tessellations

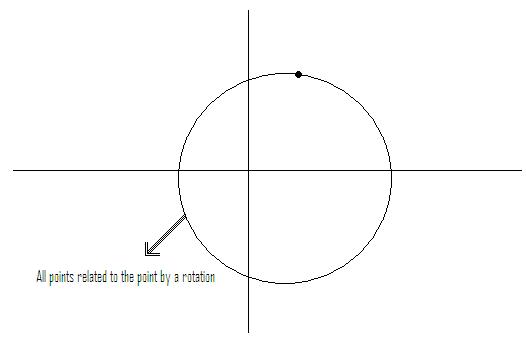
Example: if feature vectors are such that vectors related by a rotation belong to same class $ \rightarrow $ metric should be chosen so that tiles are rotationally symmetric. See Figure 2.

Figure 2 - Example of Vectors related by Rotations

Instead of working with (x,y) rotationally invariant, work with $ z=\sqrt{x^2 + y^2} $ (distance from origin)

How good is Nearest Neighbor rule?

1. Training error is zero: does not measure the "goodness" of a rule
2. Test error: want it to be equal to Bayes error rate, because this yields the minimum error

Nearest Neighbor error rate

Recall: Probability of error (error rate) on test data is $ P(e)=\int p(e \mid \vec{x}) p(\vec{x}) d\vec{x} $

Let $ P_d(e) $ be the error rate when d training samples are used.

Let $ P=\lim_{d \rightarrow \infty } P_{d}(e) $

Claim: limit error rate $ P=\int (1-\sum _{i=1} ^{c}p^2 (\omega _i \mid \vec{x}))p(x)dx $

Proof of claim: Given observation $ \vec{x} $, denode by $ \vec{x'}_d $ the nearest neighbor of $ \vec{x} $ among $ \{\vec{x}_1,\vec{x}_2, \cdots , \vec{x}_d \} $

$ P_d(e \mid \vec{x})=\int p_d(e \mid \vec{x}, \vec{x'}_d)p_d(\vec{x'}_d \mid \vec{x})p(x)dx $ but $ \lim _{d \rightarrow \infty } p_d (\vec{x'}_d \mid \vec{x})=\delta ({\vec{x' _d }-\vec{x}}) $

because probability that sample falls into region R centered at $ \vec{x} $ is $ P_{R}=\int _R p(\vec{x' _d})d \vec{x'}_d $.

So, if $ p(\vec{x}) \neq 0 $ (true almost everywhere), then probability that all samples fall outside R is $ \lim _{d \rightarrow \infty} {(1-P_{R})}^d =0 $

So, $ \lim _{d \rightarrow \infty} \vec{x'}_d = \vec{x} $ and $ p_d (\vec{x'}_d \mid \vec{x})=\delta (\vec{x'}_d -\vec{x})+\epsilon _d (\vec{x}) $ where $ \lim _{d \rightarrow \infty } \epsilon _d (x)=0 $

Now $ p_d (e \mid \vec{x}, \vec{x'}_d) $ = ?

Let $ \theta , \theta _1 , \theta _2 , \cdots, \theta _{d} $ be the class of $ x , x_1 , x_2 , \cdots , x_d $, respectively.

Using nearest neighbor rule, error if $ \theta \neq $class of $ \vec{x'}_d $$ =: \theta ' _d $

$ \Rightarrow p_d(e \mid \vec{x},\vec{x'}_d)=1-\sum_{i=1} ^ c p(\theta = \omega _i , \theta ' _d = \omega _i \mid \vec{x}, \vec{x'}_d ) $

$ =1- \sum _{i=1} ^c p(\omega _i \mid \vec{x}) p(\omega _i \mid \vec{x'} _d) $

Recall $ p_d (e \mid \vec{x}, \vec{x'}_d)p_d (\vec{x'}_d \mid \vec{x})d \vec{x'}_d $

You get: $ p_d (e \mid \vec{x})=(1-\sum _{i=1} ^c p(\omega _i \mid x) p(\omega _i \mid x) ) $ + {something that goes to zero as d goes to $ \infty $}

$ \lim _{d \rightarrow \infty} p_d (e \mid \vec{x})=(1- \sum _{i=1} ^c {p(\omega _i \mid x)}^2) $

Previous: Lecture 17 Next: Lecture 19

Back to ECE662 Spring 2008 Prof. Boutin