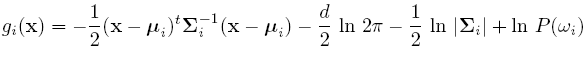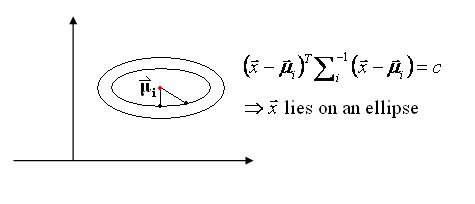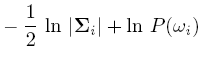| (28 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | [ | + | [[Category:ECE662]] |
| + | [[Category:decision theory]] | ||
| + | [[Category:lecture notes]] | ||
| + | [[Category:pattern recognition]] | ||
| + | [[Category:slecture]] | ||
| + | <center><font size= 4> | ||
| + | '''[[ECE662]]: Statistical Pattern Recognition and Decision Making Processes''' | ||
| + | </font size> | ||
| + | |||
| + | Spring 2008, [[user:mboutin|Prof. Boutin]] | ||
| + | |||
| + | [[Slectures|Slecture]] | ||
| + | |||
| + | <font size= 3> Collectively created by the students in [[ECE662:BoutinSpring08_OldKiwi|the class]]</font size> | ||
| + | </center> | ||
| + | |||
| + | ---- | ||
| + | =Lecture 5 Lecture notes= | ||
| + | Jump to: [[ECE662_Pattern_Recognition_Decision_Making_Processes_Spring2008_sLecture_collective|Outline]]| | ||
| + | [[Lecture 1 - Introduction_OldKiwi|1]]| | ||
| + | [[Lecture 2 - Decision Hypersurfaces_OldKiwi|2]]| | ||
| + | [[Lecture 3 - Bayes classification_OldKiwi|3]]| | ||
| + | [[Lecture 4 - Bayes Classification_OldKiwi|4]]| | ||
| + | [[Lecture 5 - Discriminant Functions_OldKiwi|5]]| | ||
| + | [[Lecture 6 - Discriminant Functions_OldKiwi|6]]| | ||
| + | [[Lecture 7 - MLE and BPE_OldKiwi|7]]| | ||
| + | [[Lecture 8 - MLE, BPE and Linear Discriminant Functions_OldKiwi|8]]| | ||
| + | [[Lecture 9 - Linear Discriminant Functions_OldKiwi|9]]| | ||
| + | [[Lecture 10 - Batch Perceptron and Fisher Linear Discriminant_OldKiwi|10]]| | ||
| + | [[Lecture 11 - Fischer's Linear Discriminant again_OldKiwi|11]]| | ||
| + | [[Lecture 12 - Support Vector Machine and Quadratic Optimization Problem_OldKiwi|12]]| | ||
| + | [[Lecture 13 - Kernel function for SVMs and ANNs introduction_OldKiwi|13]]| | ||
| + | [[Lecture 14 - ANNs, Non-parametric Density Estimation (Parzen Window)_OldKiwi|14]]| | ||
| + | [[Lecture 15 - Parzen Window Method_OldKiwi|15]]| | ||
| + | [[Lecture 16 - Parzen Window Method and K-nearest Neighbor Density Estimate_OldKiwi|16]]| | ||
| + | [[Lecture 17 - Nearest Neighbors Clarification Rule and Metrics_OldKiwi|17]]| | ||
| + | [[Lecture 18 - Nearest Neighbors Clarification Rule and Metrics(Continued)_OldKiwi|18]]| | ||
| + | [[Lecture 19 - Nearest Neighbor Error Rates_OldKiwi|19]]| | ||
| + | [[Lecture 20 - Density Estimation using Series Expansion and Decision Trees_OldKiwi|20]]| | ||
| + | [[Lecture 21 - Decision Trees(Continued)_OldKiwi|21]]| | ||
| + | [[Lecture 22 - Decision Trees and Clustering_OldKiwi|22]]| | ||
| + | [[Lecture 23 - Spanning Trees_OldKiwi|23]]| | ||
| + | [[Lecture 24 - Clustering and Hierarchical Clustering_OldKiwi|24]]| | ||
| + | [[Lecture 25 - Clustering Algorithms_OldKiwi|25]]| | ||
| + | [[Lecture 26 - Statistical Clustering Methods_OldKiwi|26]]| | ||
| + | [[Lecture 27 - Clustering by finding valleys of densities_OldKiwi|27]]| | ||
| + | [[Lecture 28 - Final lecture_OldKiwi|28]] | ||
| + | ---- | ||
| + | ---- | ||
'''LECTURE THEME''' : | '''LECTURE THEME''' : | ||
- ''Discriminant Functions'' | - ''Discriminant Functions'' | ||
| − | |||
'''Discriminant Functions''': one way of representing classifiers | '''Discriminant Functions''': one way of representing classifiers | ||
| Line 108: | Line 155: | ||
[[Image: final_note_OldKiwi.gif]] | [[Image: final_note_OldKiwi.gif]] | ||
Figure 5 | Figure 5 | ||
| + | ---- | ||
| + | Previous: [[Lecture_4_-_Bayes_Classification_OldKiwi|Lecture 4]] | ||
| + | Next: [[Lecture_6_-_Discriminant_Functions_OldKiwi|Lecture 6]] | ||
| − | + | [[ECE662:BoutinSpring08_OldKiwi|Back to ECE662 Spring 2008 Prof. Boutin]] | |
| − | [ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
Latest revision as of 11:17, 10 June 2013
ECE662: Statistical Pattern Recognition and Decision Making Processes
Spring 2008, Prof. Boutin
Collectively created by the students in the class
Lecture 5 Lecture notes
Jump to: Outline| 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| 20| 21| 22| 23| 24| 25| 26| 27| 28
LECTURE THEME : - Discriminant Functions
Discriminant Functions: one way of representing classifiers
Given the classes $ \omega_1, \cdots, \omega_k $
The discriminant functions $ g_1(x),\ldots, g_K(x) $ such that $ g_i(x) $ n-dim S space $ \rightarrow \Re $
which are used to make decisions as follows:
decide $ \omega_i $ if $ g_i(x) \ge g_j(x), \forall j $
Note that many different choices of $ g_i(x) $ will yield the same decision rule, because we are interested in the order of values of $ g_i(x) $ for each x, and not their exact values.
For example: $ g_i(x) \rightarrow 2(g_i(x)) $ or $ g_i(x) \rightarrow ln(g_i(x)) $
In other words, we can take $ g_i(x) \rightarrow f(g_i(x)) $ for any monotonically increasing function f.
Relation to Bayes Rule
e.g. We can take $ g_i(\mathbf(x)) = P(\omega_i|\mathbf(x)) $
then $ g_i(\mathbf(x)) > g_j(\mathbf(x)), \forall j \neq i $
$ \Longleftrightarrow P(w_i|\mathbf(X)) > P(w_j|\mathbf(X)), \forall j \neq i $
OR we can take
$ g_i(\mathbf(x)) = p(\mathbf(x)|\omega_i)P(\omega_i) $
then $ g_i(\mathbf(x)) > g_j(\mathbf(x)), \forall j \neq i $
$ \Longleftrightarrow g_i(\mathbf(x)) = ln(p(\mathbf(x)|\omega_i)P(\omega_i)) = ln(p(\mathbf(x)|\omega_i))+ln(P(\omega_i) $
OR we can take
$ g_i(\mathbf(x)) = ln(p(\mathbf(x)|\omega_i)P(\omega_i)) = ln(p(\mathbf(x)|\omega_i))+ln(P(\omega_i) $
We can take any $ g_i $ as long as they have the same ordering in value as specified by Bayes rule.
Some useful links:
- Bayes Rule in notes: https://engineering.purdue.edu/people/mireille.boutin.1/ECE301kiwi/Lecture4
- Bayesian Inference: http://en.wikipedia.org/wiki/Bayesian_inference
Relational Decision Boundary
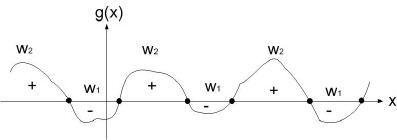
Ex : take two classes $ \omega_1 $ and $ \omega_2 $
$ g(\vec x)=g_1(\vec x)-g_2(\vec x) $
decide $ \omega_1 $ when $ g(\vec x)>0 $
and $ \omega_2 $ when $ g(\vec x)<0 $
when $ g(\vec x) = 0 $, you are at the decision boundary ( = hyperplane)
$ \lbrace \vec x | \vec x \;\;s.t \;\;g(\vec x)=0\rbrace $ is a hypersurface in your feature space i.e a structure of co-dimension one less dimension than space in which $ \vec x $ lies
Discriminant function for the Normal Density
Suppose we assume that the distribution of the feature vectors is such that the density function p(X|w) is normal for all i.
Eg: Length of hair among men is a normal random variable. Same for hairlength in women. Now we have:
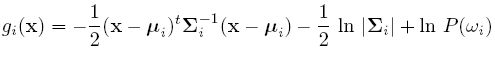
For simplicity, add n/2ln(2pi) to all gi's. Then we get:
If classes are equally likely, then we can get rid of the first term.
If the Distribution Matrix is the same, then the second term goes off.
Special case 1: "Spherical clusters" in n-dimensional space. Equidistant points lie on a circle around the average values.
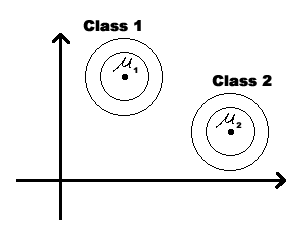 Figure 3
Figure 3
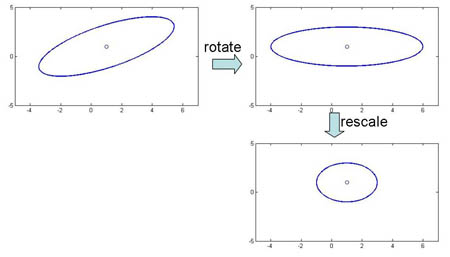
Final Note on Lecture 5:
We could modify the coordinates of a class feature vector (as shown on the figure below) to take advantage of Special Case 1. But you should be aware that, in general, this can not be done for all classes simultaneously.