| (4 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| + | [[Category:Problem_solving]] | ||
| + | [[Category:ECE438]] | ||
| + | [[Category:digital signal processing]] | ||
| + | |||
| + | =Quiz Pool for Week 6, [[ECE438]] lab, Fall 2010== | ||
<math>\text{ Sample a continuous signal x(t)=sin(}\omega t)\text{ with period of T, }</math> | <math>\text{ Sample a continuous signal x(t)=sin(}\omega t)\text{ with period of T, }</math> | ||
| Line 19: | Line 24: | ||
Assume that the input signal X(f) and the continuous time filter H(f) are both band limited to 1/(2T). | Assume that the input signal X(f) and the continuous time filter H(f) are both band limited to 1/(2T). | ||
| − | 3. <math>\text{Compute expressions for Y} (e^{j\omega})\text{ and | + | 3. <math>\text{Compute expressions for Y} (e^{j\omega})\text{ and Z}(e^{j\omega})</math>. |
4. Show that when | 4. Show that when | ||
| − | <math>G(e^{j\omega}) = \sum_{ | + | <math>G(e^{j\omega}) = \sum_{k=-\infty}^{\infty} H \Bigg( \frac{\omega - 2k\pi}{2k\pi}\Bigg)</math> |
then the output of the two systems is equal. | then the output of the two systems is equal. | ||
| Line 33: | Line 38: | ||
5. The following system shows an interpolator with discrete input x[n]. Assume that the low pass filter has frequency response | 5. The following system shows an interpolator with discrete input x[n]. Assume that the low pass filter has frequency response | ||
| − | <math> H(e^{j\omega}) = | + | <math> H(e^{j\omega}) = 2\text{rect}(\omega / \pi ) \text{ for } \left | \omega \right | < \pi </math>. |
[[Image:Upsample.jpg]] | [[Image:Upsample.jpg]] | ||
| Line 45: | Line 50: | ||
<math>\text{c. }x[n] = 1</math> | <math>\text{c. }x[n] = 1</math> | ||
| − | <math>\text{d. }x[n] = cos | + | <math>\text{d. }x[n] = cos (\pi n/4)</math> |
Answer [[ECE438_Week6_Quiz_Q5sol|here]]. | Answer [[ECE438_Week6_Quiz_Q5sol|here]]. | ||
| Line 53: | Line 58: | ||
6. The following system shows a decimator with discrete input x[n]. Assume that the low pass filter has frequency response | 6. The following system shows a decimator with discrete input x[n]. Assume that the low pass filter has frequency response | ||
| − | <math> H(e^{j\omega}) = rect(\omega / \pi ) \text{ for } \left | \omega \right | < \pi </math>. | + | <math> H(e^{j\omega}) = \text{rect}(\omega / \pi ) \text{ for } \left | \omega \right | < \pi </math>. |
[[Image:Downsample.jpg]] | [[Image:Downsample.jpg]] | ||
Latest revision as of 09:41, 11 November 2011
Quiz Pool for Week 6, ECE438 lab, Fall 2010=
$ \text{ Sample a continuous signal x(t)=sin(}\omega t)\text{ with period of T, } $
1) In order to avoid aliasing, what is the maximum value of T? Write down the discrete time signal x(n) with the maximum T. Answer here.
2) The system diagram is as follows.
In order to get rid of aliasing, what is the cut-off frequency of the low pass filter? Explain your answer. Answer here.
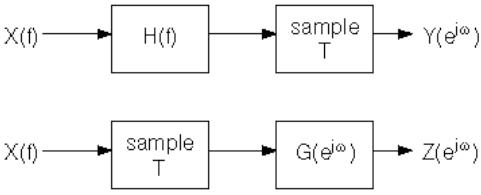
The following two systems are used to process a signal
Assume that the input signal X(f) and the continuous time filter H(f) are both band limited to 1/(2T).
3. $ \text{Compute expressions for Y} (e^{j\omega})\text{ and Z}(e^{j\omega}) $.
4. Show that when
$ G(e^{j\omega}) = \sum_{k=-\infty}^{\infty} H \Bigg( \frac{\omega - 2k\pi}{2k\pi}\Bigg) $
then the output of the two systems is equal.
Answer here.
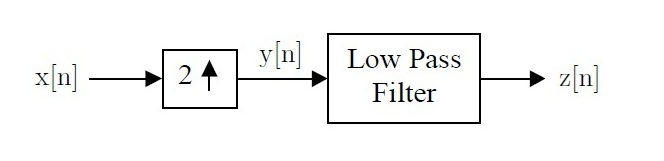
5. The following system shows an interpolator with discrete input x[n]. Assume that the low pass filter has frequency response
$ H(e^{j\omega}) = 2\text{rect}(\omega / \pi ) \text{ for } \left | \omega \right | < \pi $.
Compute the z[n] for the following inputs.
$ \text{a. }x[n] = \delta [n] $
$ \text{b. }x[n] = \delta [n-1] $
$ \text{c. }x[n] = 1 $
$ \text{d. }x[n] = cos (\pi n/4) $
Answer here.
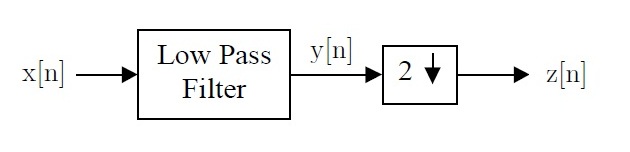
6. The following system shows a decimator with discrete input x[n]. Assume that the low pass filter has frequency response
$ H(e^{j\omega}) = \text{rect}(\omega / \pi ) \text{ for } \left | \omega \right | < \pi $.
Compute the z[n] for the following inputs.
$ \text{a. }x[n] = \delta [n] $
$ \text{b. }x[n] = \delta [n-1] $
$ \text{c. }x[n] = 1 $
$ \text{d. }x[n] = cos (\pi n/4) $
Answer here.