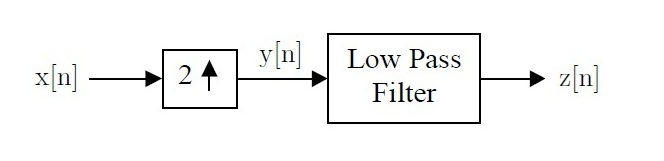
Solution to Q5 of Week 6 Quiz Pool
$ \begin{align} \text{(a)} \quad & x[n] = \delta[n] \\ & X(e^{jw}) = 1 \;\; \text{for} \;\; w \in (-\pi,\pi) \\ & Y(e^{jw}) = X(e^{j2w}) = 1 \;\; \text{for} \;\; w \in (-\pi,\pi) \\ & Z(e^{jw}) = Y(e^{jw}) \times 2\text{rect}\Big(\frac{w}{\pi}\Big) = 2\text{rect}\Big(\frac{w}{\pi}\Big) \;\; \text{for} \;\; w \in (-\pi,\pi) \\ & z[n] = 2\frac{\text{sin}\big(\frac{\pi}{2}n\big)}{\pi n} \\ \end{align} \,\! $
$ \begin{align} \text{(b)} \quad & x[n] = \delta[n-1] \\ & X(e^{jw}) = e^{-jw}(1) \;\; \text{for} \;\; w \in (-\pi,\pi) \\ & Y(e^{jw}) = X(e^{j2w}) = e^{-j2w}(1) \;\; \text{for} \;\; w \in (-\pi,\pi) \\ & Z(e^{jw}) = Y(e^{jw}) \times 2\text{rect}\Big(\frac{w}{\pi}\Big) = e^{-j2w} \bigg( 2\text{rect}\Big(\frac{w}{\pi}\Big) \bigg) \;\; \text{for} \;\; w \in (-\pi,\pi) \\ & z[n] = 2\frac{\text{sin}\big(\frac{\pi}{2}(n-2)\big)}{\pi(n-2)} \\ \end{align} \,\! $
Note that, since it is upsampled by a factor of 2, $ z[n] $ is shifted 2 to the right compared to $ z[n] $ of (a), even though the input $ x[n] $ is shifted 1 to the right compared to the input $ x[n] $ of (a).
$ \begin{align} \text{(c)} \quad & x[n] = 1 \\ & X(e^{jw}) = 2\pi\delta(w) \;\; \text{for} \;\; w \in (-\pi,\pi) \\ & Y(e^{jw}) = X(e^{j2w}) = 2\pi\delta(2w) = \pi\delta(w) \;\; \text{for} \;\; w \in (-\pi,\pi), \; \text{since} \; k\delta(kw)=\delta(w), \; \forall \; k\neq0 \\ & Z(e^{jw}) = Y(e^{jw}) \times 2\text{rect}\Big(\frac{w}{\pi}\Big) = \pi\delta(w) \bigg( 2\text{rect}\Big(\frac{w}{\pi}\Big) \bigg) = 2\pi\delta(w) \;\; \text{for} \;\; w \in (-\pi,\pi) \\ & z[n] = 1 \\ \end{align} \,\! $
$ \begin{align} \text{(d)} \quad & x[n] = \text{cos}\big(\frac{\pi}{4}n\big) \\ & X(e^{jw}) = \pi \Big[ \delta \big( w - \frac{\pi}{4} \big) + \delta \big( w + \frac{\pi}{4} \big) \Big] \;\; \text{for} \;\; w \in (-\pi,\pi) \\ & Y(e^{jw}) = X(e^{j2w}) = \pi \Big[ \delta \big( 2w - \frac{\pi}{4} \big) + \delta \big( 2w + \frac{\pi}{4} \big) \Big] \\ & \quad\quad\quad = \pi \Big[ \delta \big( 2 (w - \frac{\pi}{8}) \big) + \delta \big( 2 (w + \frac{\pi}{8}) \big) \Big] = \frac{\pi}{2} \Big[ \delta \big( w - \frac{\pi}{8} \big) + \delta \big( w + \frac{\pi}{8} \big) \Big] \;\; \text{for} \;\; w \in (-\pi,\pi) \\ & \quad\quad\quad\quad\quad \text{since} \; k\delta(kw)=\delta(w), \; \forall \; k\neq0 \\ & Z(e^{jw}) = Y(e^{jw}) \times 2\text{rect}\Big(\frac{w}{\pi}\Big) = \frac{\pi}{2} \Big[ \delta \big( w - \frac{\pi}{8} \big) + \delta \big( w + \frac{\pi}{8} \big) \Big] \bigg( 2\text{rect}\Big(\frac{w}{\pi}\Big) \bigg) \\ & \quad\quad\quad = \pi \Big[ \delta \big( w - \frac{\pi}{8} \big) + \delta \big( w + \frac{\pi}{8} \big) \Big] \;\; \text{for} \;\; w \in (-\pi,\pi) \\ & z[n] = \text{cos}\big(\frac{\pi}{8}n\big) \\ \end{align} \,\! $
Credit: Prof. Charles Bouman
Back to Lab Week 6 Quiz Pool
Back to ECE 438 Fall 2010 Lab Wiki Page
Back to ECE 438 Fall 2010