(New page: <math>\text{ Sample a continuous signal x(t)=sin(}\omega t)\text{ with period of T, }</math> 1) In order to avoid aliasing, what is the maximum value of T? Write down the discrete time s...) |
|||
| (8 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| + | [[Category:Problem_solving]] | ||
| + | [[Category:ECE438]] | ||
| + | [[Category:digital signal processing]] | ||
| + | |||
| + | =Quiz Pool for Week 6, [[ECE438]] lab, Fall 2010== | ||
<math>\text{ Sample a continuous signal x(t)=sin(}\omega t)\text{ with period of T, }</math> | <math>\text{ Sample a continuous signal x(t)=sin(}\omega t)\text{ with period of T, }</math> | ||
| Line 10: | Line 15: | ||
In order to get rid of aliasing, what is the cut-off frequency of the low pass filter? Explain your answer. | In order to get rid of aliasing, what is the cut-off frequency of the low pass filter? Explain your answer. | ||
Answer [[ECE438_Week6_Quiz_Q2sol|here]]. | Answer [[ECE438_Week6_Quiz_Q2sol|here]]. | ||
| + | |||
| + | ---- | ||
| + | |||
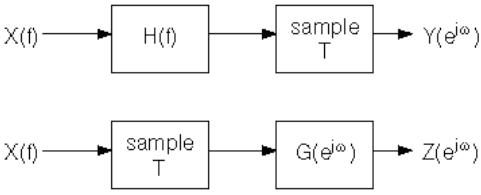
| + | The following two systems are used to process a signal | ||
| + | |||
| + | [[Image:ECE438SystemSampling.jpg]] | ||
| + | |||
| + | Assume that the input signal X(f) and the continuous time filter H(f) are both band limited to 1/(2T). | ||
| + | |||
| + | 3. <math>\text{Compute expressions for Y} (e^{j\omega})\text{ and Z}(e^{j\omega})</math>. | ||
| + | |||
| + | 4. Show that when | ||
| + | |||
| + | <math>G(e^{j\omega}) = \sum_{k=-\infty}^{\infty} H \Bigg( \frac{\omega - 2k\pi}{2k\pi}\Bigg)</math> | ||
| + | |||
| + | then the output of the two systems is equal. | ||
| + | |||
| + | Answer [[ECE438_Week6_Quiz_Q3_Q4sol|here]]. | ||
| + | |||
| + | ---- | ||
| + | |||
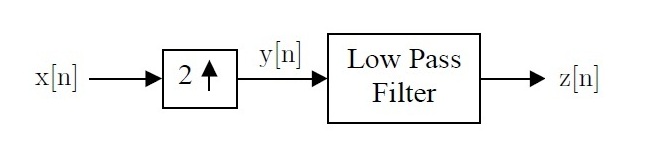
| + | 5. The following system shows an interpolator with discrete input x[n]. Assume that the low pass filter has frequency response | ||
| + | |||
| + | <math> H(e^{j\omega}) = 2\text{rect}(\omega / \pi ) \text{ for } \left | \omega \right | < \pi </math>. | ||
| + | |||
| + | [[Image:Upsample.jpg]] | ||
| + | |||
| + | Compute the z[n] for the following inputs. | ||
| + | |||
| + | <math>\text{a. }x[n] = \delta [n]</math> | ||
| + | |||
| + | <math>\text{b. }x[n] = \delta [n-1]</math> | ||
| + | |||
| + | <math>\text{c. }x[n] = 1</math> | ||
| + | |||
| + | <math>\text{d. }x[n] = cos (\pi n/4)</math> | ||
| + | |||
| + | Answer [[ECE438_Week6_Quiz_Q5sol|here]]. | ||
| + | |||
| + | ---- | ||
| + | |||
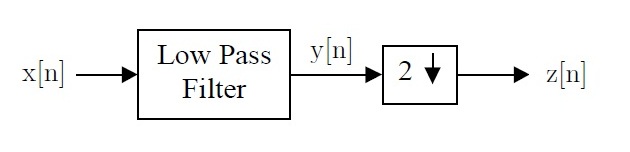
| + | 6. The following system shows a decimator with discrete input x[n]. Assume that the low pass filter has frequency response | ||
| + | |||
| + | <math> H(e^{j\omega}) = \text{rect}(\omega / \pi ) \text{ for } \left | \omega \right | < \pi </math>. | ||
| + | |||
| + | [[Image:Downsample.jpg]] | ||
| + | |||
| + | Compute the z[n] for the following inputs. | ||
| + | |||
| + | <math>\text{a. }x[n] = \delta [n]</math> | ||
| + | |||
| + | <math>\text{b. }x[n] = \delta [n-1]</math> | ||
| + | |||
| + | <math>\text{c. }x[n] = 1</math> | ||
| + | |||
| + | <math>\text{d. }x[n] = cos (\pi n/4)</math> | ||
| + | |||
| + | Answer [[ECE438_Week6_Quiz_Q6sol|here]]. | ||
| + | |||
| + | |||
| + | |||
| + | --------------------------------------------------------------------- | ||
| + | [[ECE438_Lab_Fall_2010|Back to Lab Wiki]] | ||
Latest revision as of 09:41, 11 November 2011
Quiz Pool for Week 6, ECE438 lab, Fall 2010=
$ \text{ Sample a continuous signal x(t)=sin(}\omega t)\text{ with period of T, } $
1) In order to avoid aliasing, what is the maximum value of T? Write down the discrete time signal x(n) with the maximum T. Answer here.
2) The system diagram is as follows.
In order to get rid of aliasing, what is the cut-off frequency of the low pass filter? Explain your answer. Answer here.
The following two systems are used to process a signal
Assume that the input signal X(f) and the continuous time filter H(f) are both band limited to 1/(2T).
3. $ \text{Compute expressions for Y} (e^{j\omega})\text{ and Z}(e^{j\omega}) $.
4. Show that when
$ G(e^{j\omega}) = \sum_{k=-\infty}^{\infty} H \Bigg( \frac{\omega - 2k\pi}{2k\pi}\Bigg) $
then the output of the two systems is equal.
Answer here.
5. The following system shows an interpolator with discrete input x[n]. Assume that the low pass filter has frequency response
$ H(e^{j\omega}) = 2\text{rect}(\omega / \pi ) \text{ for } \left | \omega \right | < \pi $.
Compute the z[n] for the following inputs.
$ \text{a. }x[n] = \delta [n] $
$ \text{b. }x[n] = \delta [n-1] $
$ \text{c. }x[n] = 1 $
$ \text{d. }x[n] = cos (\pi n/4) $
Answer here.
6. The following system shows a decimator with discrete input x[n]. Assume that the low pass filter has frequency response
$ H(e^{j\omega}) = \text{rect}(\omega / \pi ) \text{ for } \left | \omega \right | < \pi $.
Compute the z[n] for the following inputs.
$ \text{a. }x[n] = \delta [n] $
$ \text{b. }x[n] = \delta [n-1] $
$ \text{c. }x[n] = 1 $
$ \text{d. }x[n] = cos (\pi n/4) $
Answer here.