| (5 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
[[Category:2010 Fall ECE 438 Boutin]] | [[Category:2010 Fall ECE 438 Boutin]] | ||
| + | [[Category:Problem_solving]] | ||
| + | [[Category:ECE438]] | ||
| + | [[Category:digital signal processing]] | ||
---- | ---- | ||
| Line 16: | Line 19: | ||
* [[ECE438_Week10_Quiz_Q1sol|Solution]]. | * [[ECE438_Week10_Quiz_Q1sol|Solution]]. | ||
---- | ---- | ||
| − | Q2. | + | Q2. The condition for the discrete-time signal <math>x[n]</math> to be real is |
| − | + | <math> x[n]=x^{\ast}[n] </math> | |
| − | + | Then, what is the condition of the frequency response <math>X(w)</math> for <math>x[n]</math> to be real? | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | Then, what is the condition of the frequency response <math> | + | |
(Hint: Apply DTFT to the above equation) | (Hint: Apply DTFT to the above equation) | ||
| Line 31: | Line 30: | ||
---- | ---- | ||
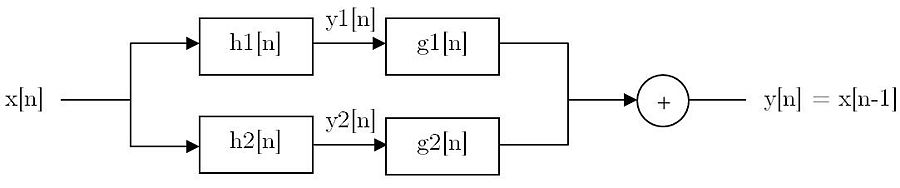
Q3. | Q3. | ||
| + | [[Image:Qp10q3system.jpg|900px]] | ||
| + | |||
| + | The respective difference equation for each of these two systems in parallel above may be expressed as | ||
| + | |||
| + | y1[n] = ½ x[n] + ½ x[n-1] <br/> | ||
| + | y2[n] = ½ x[n] - ½ x[n-1] <br/> | ||
| + | |||
| + | Consider the respective outputs of these two systems as the inputs to a pair of length two FIR filters with impulse response, g1[n] and g2[n] respectively, as shown in the diagram. | ||
| + | |||
| + | a. Given that g1[0] = ½, determine the values of g1[n] and g2[n], where n = 0, 1, such that the difference equation for the overall system is simply | ||
| + | |||
| + | y[n] = x[n-1] | ||
| + | |||
| + | That is, determine length-2 FIR filters g1[n] and g2[n] so that output is the input delayed by one (for any input). | ||
| + | |||
| + | b. Let H(<math>\omega</math>) denote the frequency response of the overall system equal to the DTFT of h[n] below: | ||
| + | |||
| + | h[n] = h1[n] * g1[n] + h2[n] * g2[n] | ||
| + | |||
| + | Plot both the magnitude H(<math>\omega</math>) and the phase H(<math>\omega</math>) over -<math>\pi</math> < <math>\omega</math> < <math>\pi</math>. | ||
* [[ECE438_Week10_Quiz_Q3sol|Solution]]. | * [[ECE438_Week10_Quiz_Q3sol|Solution]]. | ||
---- | ---- | ||
| − | Q4. | + | Q4. Given a LTI system, when the input is |
| + | <math>x[n]=(\frac{1}{2})^nu[n]+2^nu[-n-1]</math> | ||
| + | |||
| + | the output is | ||
| + | <math>y[n]=6(\frac{1}{2})^nu[n]-6(\frac{3}{4})^nu[n]</math> | ||
| + | |||
| + | a. Compute the transfer function. Plot the zero-pole graph of H(z) and declare the ROC. | ||
| + | |||
| + | b. Compute the impulse response h[n] of the system. | ||
| + | |||
| + | c. Obtain the difference equation represents the system. | ||
| + | |||
| + | d. Determineif the filter represented by the difference equation is FIR or IIR. Give reasons for your choice. | ||
| + | |||
| + | e. Is the system stable? Explain why or why not. | ||
* [[ECE438_Week10_Quiz_Q4sol|Solution]]. | * [[ECE438_Week10_Quiz_Q4sol|Solution]]. | ||
---- | ---- | ||
| − | |||
| − | |||
| − | |||
Back to [[ECE438_Lab_Fall_2010|ECE 438 Fall 2010 Lab Wiki Page]] | Back to [[ECE438_Lab_Fall_2010|ECE 438 Fall 2010 Lab Wiki Page]] | ||
Back to [[2010_Fall_ECE_438_Boutin|ECE 438 Fall 2010]] | Back to [[2010_Fall_ECE_438_Boutin|ECE 438 Fall 2010]] | ||
Latest revision as of 09:42, 11 November 2011
Quiz Questions Pool for Week 10
Q1. Consider the following difference equation
- $ y[n]=ay[n-1]+x[n]-x[n-1]\,\! $
- a. Compute the transfer function $ H(z) $, and find its poles and zeros.
- b. Compute the impulse response $ h[n] $ using a ROC of $ |z|>a $. For what values of $ a $ is the system stable?
- c. Compute the impulse response $ h[n] $ using a ROC of $ |z|<a $. For what values of $ a $ is the system stable?
Q2. The condition for the discrete-time signal $ x[n] $ to be real is
$ x[n]=x^{\ast}[n] $
Then, what is the condition of the frequency response $ X(w) $ for $ x[n] $ to be real?
(Hint: Apply DTFT to the above equation)
The respective difference equation for each of these two systems in parallel above may be expressed as
y1[n] = ½ x[n] + ½ x[n-1]
y2[n] = ½ x[n] - ½ x[n-1]
Consider the respective outputs of these two systems as the inputs to a pair of length two FIR filters with impulse response, g1[n] and g2[n] respectively, as shown in the diagram.
a. Given that g1[0] = ½, determine the values of g1[n] and g2[n], where n = 0, 1, such that the difference equation for the overall system is simply
y[n] = x[n-1]
That is, determine length-2 FIR filters g1[n] and g2[n] so that output is the input delayed by one (for any input).
b. Let H($ \omega $) denote the frequency response of the overall system equal to the DTFT of h[n] below:
h[n] = h1[n] * g1[n] + h2[n] * g2[n]
Plot both the magnitude H($ \omega $) and the phase H($ \omega $) over -$ \pi $ < $ \omega $ < $ \pi $.
Q4. Given a LTI system, when the input is $ x[n]=(\frac{1}{2})^nu[n]+2^nu[-n-1] $
the output is $ y[n]=6(\frac{1}{2})^nu[n]-6(\frac{3}{4})^nu[n] $
a. Compute the transfer function. Plot the zero-pole graph of H(z) and declare the ROC.
b. Compute the impulse response h[n] of the system.
c. Obtain the difference equation represents the system.
d. Determineif the filter represented by the difference equation is FIR or IIR. Give reasons for your choice.
e. Is the system stable? Explain why or why not.
Back to ECE 438 Fall 2010 Lab Wiki Page
Back to ECE 438 Fall 2010