| Line 27: | Line 27: | ||
---- | ---- | ||
Q3. | Q3. | ||
| + | [[Image:Qp10q3system.jpg]] | ||
| + | |||
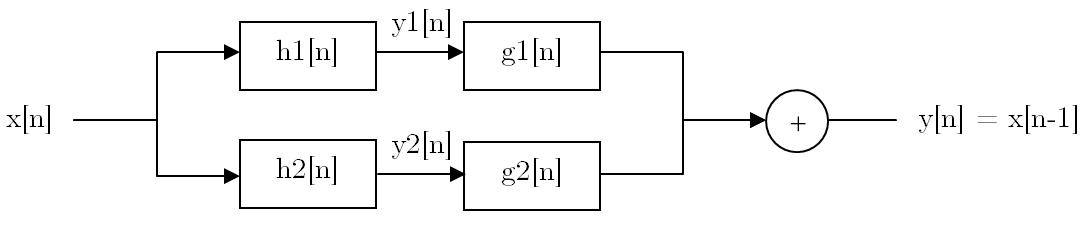
| + | The respective difference equation for each of these two systems in parallel above may be expressed as | ||
| + | |||
| + | y1[n] = ½ x[n] + ½ x[n-1] <br/> | ||
| + | y2[n] = ½ x[n] - ½ x[n-1] <br/> | ||
| + | |||
| + | Consider the respective outputs of these two systems as the inputs to a pair of length two FIR filters with impulse response, g1[n] and g2[n] respectively, as shown in the diagram. | ||
| + | |||
| + | a. Given that g1[0] = ½, determine the values of g1[n] and g2[n], where n = 0, 1, such that the difference equation for the overall system is simply | ||
| + | |||
| + | y[n] = x[n-1] | ||
| + | |||
| + | That is, determine length-2 FIR filters g1[n] and g2[n] so that output is the input delayed by one (for any input). | ||
| + | |||
| + | b. Let H(\omega) denote the frequency response of the overall system equal to the DTFT of h[n] below: | ||
| + | |||
| + | h[n] = h1[n] * g1[n] + h2[n] * g2[n] | ||
| + | |||
| + | Plot both the magnitude H(<math>\omega</math>) and the phase H(<math>\omega</math>) over -<math>\pi</math> < <math>\omega</math> < <math>\pi</math>. | ||
* [[ECE438_Week10_Quiz_Q3sol|Solution]]. | * [[ECE438_Week10_Quiz_Q3sol|Solution]]. | ||
Revision as of 13:33, 27 October 2010
Quiz Questions Pool for Week 10
Q1. Consider the following difference equation
- $ y[n]=ay[n-1]+x[n]-x[n-1]\,\! $
- a. Compute the transfer function $ H(z) $, and find its poles and zeros.
- b. Compute the impulse response $ h[n] $ using a ROC of $ |z|>a $. For what values of $ a $ is the system stable?
- c. Compute the impulse response $ h[n] $ using a ROC of $ |z|<a $. For what values of $ a $ is the system stable?
Q2. The condition for the discrete-time signal $ x[n] $ to be real is
$ x[n]=x^{\ast}[n] $
Then, what is the condition of the frequency response $ X(w) $ for $ x[n] $ to be real?
(Hint: Apply DTFT to the above equation)
The respective difference equation for each of these two systems in parallel above may be expressed as
y1[n] = ½ x[n] + ½ x[n-1]
y2[n] = ½ x[n] - ½ x[n-1]
Consider the respective outputs of these two systems as the inputs to a pair of length two FIR filters with impulse response, g1[n] and g2[n] respectively, as shown in the diagram.
a. Given that g1[0] = ½, determine the values of g1[n] and g2[n], where n = 0, 1, such that the difference equation for the overall system is simply
y[n] = x[n-1]
That is, determine length-2 FIR filters g1[n] and g2[n] so that output is the input delayed by one (for any input).
b. Let H(\omega) denote the frequency response of the overall system equal to the DTFT of h[n] below:
h[n] = h1[n] * g1[n] + h2[n] * g2[n]
Plot both the magnitude H($ \omega $) and the phase H($ \omega $) over -$ \pi $ < $ \omega $ < $ \pi $.
Q4.
Q5.
Back to ECE 438 Fall 2010 Lab Wiki Page
Back to ECE 438 Fall 2010