Contents
[hide]Fractals
Harry Lee and Camber Boles
| Table of Contents |
|---|
| 1. Introduction |
| 2. Definition and Characteristics |
| 3. Generating Fractals |
| 4. Examples |
| 5. Applications |
1. Introduction
2. Definition and Characteristics
The most commonly used description for fractals is one that Benoit B. Mandelbrot published in his book, The Fractal Geometry of Nature. He says that a fractal is "a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole." Additionally, Mandelbrot is the mathematician who coined the term "fractal" in 1975, and it is derived from the Latin words fractus which means fragmented or broken. Mathematicians do not agree on a single definition, and some mathematicians are against having a strict definition. However, they do agree that there are characteristics common in most fractals that could be used to describe the concept of fractals:
Self-Similarity
If a shape has self-similarity, it means that the whole has exact or approximately the same shape as a smaller part of itself. For example, broccoli is made up of smaller parts that have a similar shape to the whole, and those smaller parts have even smaller parts that have a similar shape. However, you will also notice that the smaller parts of broccoli are not exact copies of the whole broccoli. There are different types of self-similarity and many of them describe cases where the copies are not identical.
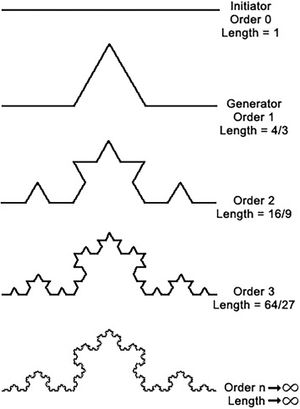
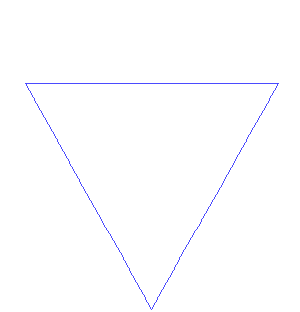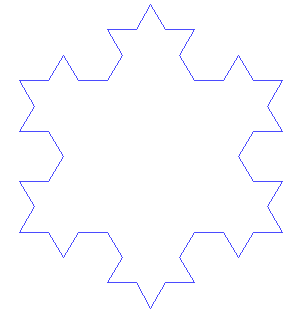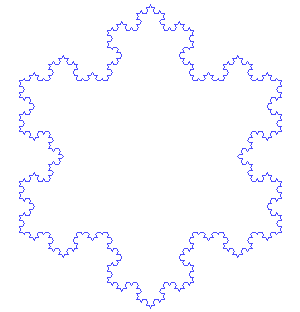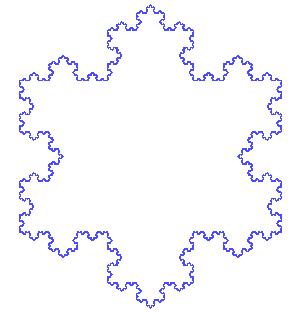
- Exact self-similarity: The whole and the smaller parts are identical. An example is the Koch Snowflake.
- Quasi self-similarity: This means that the shapes are similar but slightly different in some way. In other words, the broccoli would be an example of Quasi self-similarity. Another example in mathematics would be the Mandelbrot set.
- Statistical self-similarity: If something has statistical self-similarity, the shape might not necessarily be similar, but the statistical properties of the smaller part are similar to that of the whole. This is the case with most things in the real world with self-similarity.
- Multifractal scaling: this is when the fractal or geometry can be characterized by more than one fractal dimension (mentioned later).
Infinitely Detailed
Fractals are infinitely detailed, or in other words, they have infinitely small details. Even if you zoom continuously zoom into a fractal, you will still see smaller and smaller details. In turn, some fractals have emergent properties. A simple way of saying this is that the whole is greater than the sum of its parts. In the context of fractals, this means that the whole fractal might have properties that are independent of the incredibly small detailed parts.
Video of zooming into a fractal
Irregularity
Fractals have irregularities when zoomed in at any scale that make it extremely difficult to be described by Euclidean geometry.
Simple and Recursive Definition
Although fractals seem very complex with infinitely small details, they can often be created with very few lines of code on a computer. This is because they have simple and recursive definitions to create fractals. Recalling recursive form when working with series, recursive means that you are repeatedly applying the same rule, or definition. For example, the Mandelbrot set is defined is created by using the recursive definition, zn+1 = zn2 + c.
Fractal dimension
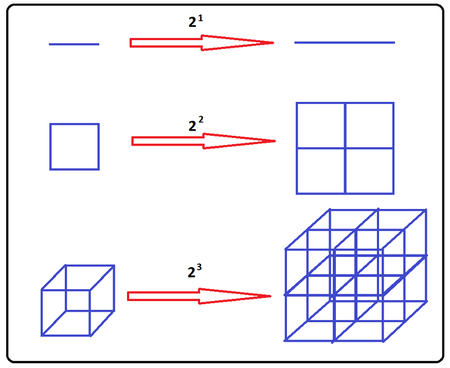
Fractal dimension is a way mathematicians use to characterize fractal patterns. Fractal dimensions are complex, and will only be briefly talked about here, but the video below gives an excellent explanation of what it is and how it can be calculated. When thinking of fractal dimensions, do not think of it in the context of the three dimensions you know, as something new. For simple shapes like a line, a square, or a box, it is easy to see define the relationship between itself, and a scaled version of itself. For example, if a line, a square, and a cube were scaled by one-half, the length of the smaller line would be one-half of the original, the area of the smaller square would be one-fourth of the original, and the volume of the smaller cube would be one-eight of the original. Similarly, fractals are made up of smaller parts of themselves. For example, the Sierpiński triangle is made up of three smaller Sierpiński triangles that have the side lengths scaled by one-half. However, there is no measurement, like length, area, or volume, that we can say is one-third of the original. For the sake of understanding, if we imagined that these are made of concrete material such as metal, we would use mass instead of length, area, or volume for the three simple shapes, and we could say that the mass of the smaller Sierpiński triangles earlier is one-third of the original.
For the three simple shapes, the mass scale factors are the power of the initial scale factor of one-half. These powers would turn out to be one for the line, two for the square, and three for the cube. Therefore, if this power was calculated for the Sierpiński Triangle, it would be about 1.585, which is its fractal dimension. So, as a way to "measure" or characterize fractal patterns, mathematicians created fractal dimension and another way to think about it is the quantitative measurement of roughness. While this gives you an idea of fractal dimensions, this explanation relies on having exact self-similarity which is often not the case of fractals and application in the real world. Therefore, there is a lot more to fractal dimensions and how they are calculated.
Here is a great video to understand fractal dimension and how it can be calculated: Fractal Dimension Explanation.
The last common characteristic of fractals is having a fractal dimension that is greater than its topological dimension. To briefly explain topological dimension, it is the dimension of the object that could be used to separate the original object into two parts. For example, the topological dimension of a line segment is one since it can be split with a point, which is 1-dimensional. Additionally, the topological dimension remains the same for homeomorphisms, or one-to-one transformations. Therefore, any shape that can be made using a piece of wire would have the topological dimension of one since they can all be transformed into another. Going back to fractals, the characteristic of having a fractal dimension greater than its topological dimension is true for most fractals, with the exception of space-filling curves such as the Hilbert curve.
3. Generating Fractals
There are many methods to generate fractals, but three of the more commonly used are escape-time fractals, iterated function systems, and random fractals.
Escape-time Fractals
This type of generating fractals is using a recurrence relation at each point in space, such as a complex plane. Some fractals that can be generated using this method are the Mandelbrot set, Julia set, Burning Ship fractal, Nova fractal, and Lyapunov fractal.
If we look at the Mandelbrot set as an example, it uses the recurrence relation, zn+1 = zn2 + c, where c is each point on a complex plane and z starts at 0.
| z0=0 | z0=1 | z0=-1 | z0=2+3i |
|---|---|---|---|
| z1=02+0=0 | z1=02+1=1 | z1=02+(-1)=-1 | z1=02+(2+3i)=2+3i |
| z2=02+0=0 | z2=12+1=2 | z2=(-1)2+(-1)=0 | z2=(2+3i)2+(2+3i)=-3+15i |
| z3=02+0=0 | z3=22+1=5 | z3=02+(-1)=-1 | z3=(-3+15i)2+(2+3i)=-214-87i |
| z4=02+0=0 | z4=52+1=26 | z4=(-1)2+(-1)=0 | z4=(-214-87i)2+(2+3i)=38229+37239i |
| z5=... | z5=... | z5=... | z5=... |
Using a couple of test cases above, we can see that as we iterate a given point, the result either stays relatively close to 0 (less than or equal to 2 in the case of the Mandelbrot set) or diverges to infinity or negative infinity. For example, for z0=0 and z0=-1, remained close to 0, while z0=1 and z0=2-3i diverged. The Mandelbrot set is the set of complex numbers for which does not result in divergence but remains bounded. When the Mandelbrot set is colored in with black, that is what creates the beautiful fractal image. However, fractal images like the one below often have multiple colors, and the different colors, especially at the border, are representing how easily divergence can be determined. In other words, it usually relies on the number of iteration it takes before divergence can be determined.
Here is a great video from Numberphile explaining the recurrence relation in the Mandelbrot set: Recurrence Relation of the Mandelbrot Set.
Iterated Function Systems
Iterated function systems use fixed geometry replacement rules, either stochastic or deterministic, to create fractals. Some Examples are Koch snowflake, Cantor set, Haferman carpet, Sierpinski carpet, Sierpinski gasket, Peano curve, Harter-Heighway dragon curve, T-square, and Menger sponge.
The images above show the generation of the Koch curve and snowflake (each side of the Koch snowflake is a Koch curve) using the iterated function systems method. The initial shape is an equilateral triangle. The middle third of each side is then taken out and replaced with two line segments that are equal length with the remaining line segments of the side. Then this is repeated again and again with the resulting smaller sides to create the Koch snowflake.
Deterministic means that everything is determined from the beginning. There is no randomness, and the exact fractal can be generated multiple times. On the contrary, stochastic means that there is randomness. The characteristics of a fractal are determined by chance, thus the same fractal can not be produced twice. Without going into too much detail, the deterministic iterated function systems result in fractals like the previous example. On the other hand, using fixed geometry replacement rules that are stochastic, can be thought of as introducing another parameter that is random. This results in a different fractal for every change in the new parameter. This could result in fractals that seem to be "blowing in the wind."
A simple example of how randomness can be introduced to iterated function systems is by randomly changing the direction of the vertex points on every replacement that happens on the Koch curve. For example, if flipping a coin was providing randomness, the coin landing head could mean the vertex points outwards while landing tails could mean the vertex points inwards.
A more detailed explanation of the random Koch curve: Random Koch Curve.
Random Fractals
Random Fractals are fractals that use stochastic rules, which simply means that each iteration is random. Some examples are Lévy flight, percolation clusters, self avoiding walks, fractal landscapes, and trajectories of Brownian motion and the Brownian tree such as dendritic fractals.
While the iterated function system fractals can be generated with some random component mixed in, such as the random Koch curve described above, some might say that it is not truly random because of the geometry replacement rules that are deterministic. Nonetheless, any fractal generated using a stochastic rule is considered a random fractal, including the stochastic iterated function system shown above. This method of generating fractals cannot create an identical fractal twice. Incorporating randomness into the generation of fractals allow modeling and simulation of natural forms, the Brownian tree modeling growth of a natural tree and fractal landscapes being able to generate random landscapes like mountains.