Contents
[hide]Third Penrose Tiling/Rhombus Tiling (P3)
For the third Penrose tiling, it only uses rhombi. As mentioned when describing the type of shapes used for different Penrose tiling, there are two different rhombi used. Both have equal sides, but different angles.
Thin Rhombus
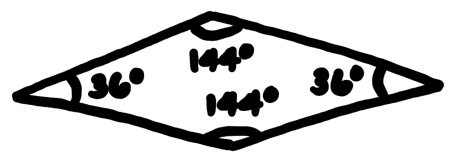
The first rhombus can be referred to as the thin rhombus, which is pictured below (Wan, 2020).
The thin rhombus has two 36° angles and two 144° angles. If the rhombus is bisected along the short diagonal, then two acute Robinson triangles are formed.
Thick Rhombus
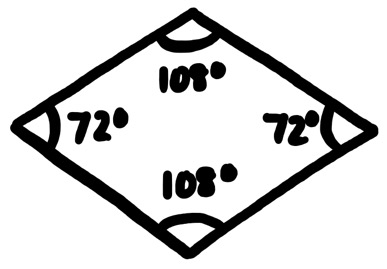
The second rhombus used in third Penrose tiling is referred to as the thick rhombus, as pictured below (Wan, 2020).
This rhombus has two 72° angles and two 108° angles. If the rhombus is bisected along the long diagonal, then two obtuse Robinson triangles are formed. If regular rhombi were put together, then it would be very possible to form periodic tiling, which would not make it Penrose tiling. Because of this situation, matching rules are put into place to avoid periodic tiling.
Matching Rules for Third Penrose Tiling (P3)
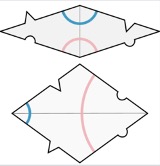
One way to approach the matching rules for third Penrose tiling is by drawing arcs of two different colors on the inside of both types of rhombi, similar to what was done for the second Penrose tiling with the kites and darts. These arcs are pictured below (Wikipedia).
Once again, similar to one of the methods in approaching the matching rules for the second Penrose tiling, when combining the thin and thick rhombi, the arcs of the same color have to make smooth, continuous lines. This prevents any periodic tiling from forming and maintains that the end result is an example of Penrose tiling. Another method in approaching the matching rules for the third Penrose tiling is by matching the "key" and "lock." Notice how some sides have a triangle or semi-circle that juts out and others have an indentation of a triangle or semi-circle. In order to successfully piece the thin and thick rhombi together, a triangle that juts out has to fit into a triangle that is indented and the same applies to the semi-circle. The key and lock analogy can be used to picture all the pieces locking together and fitting smoothly into place.
Previous Section: Second Penrose Tiling/Kite and Dart Tiling (P2)