Contents
[hide]Second Penrose Tiling/Kite and Dart Tiling (P2)
The second Penrose tiling uses only kites and darts.
Kite
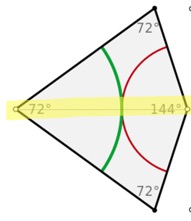
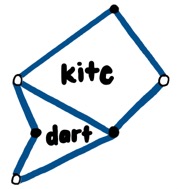
An example of a kite is pictured below (Wikipedia).
As seen in the diagram, a kite has three angles of 72° and one angle of 144°. When the kite is bisected along its axis of symmetry, as highlighted in yellow, it can form two acute Robinson triangles, which is further discussed in the Robinson Triangles section.
Dart
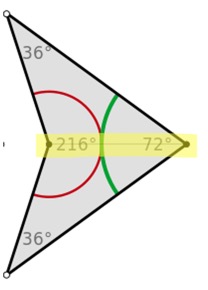
An example of a dart is pictured below (Wikipedia).
A dart is composed of two 36° angles, one 72° angle, and one 216° angle. When bisected along its axis of symmetry, as highlighted in yellow, it also forms two Robinson triangles, except they are obtuse.
Matching Rules for Second Penrose Tiling (P2)
If a kite and dart are put together with the 144° angle of the kite and 216° angle of the dart touching, a rhombus will be formed, but then this would result in periodic tiling, which is not characteristic of and a requirement for Penrose tiling. In order to avoid the formation of a rhombus, matching rules are put into place. One way to make a second Penrose tiling is by color coding the vertices of the kite and dart using two colors (i.e. black and white). If the vertices of the kite along the axis of symmetry are color-coded Color A, then the other two vertices should be color-coded Color B. In turn, the vertices of the dart along the axis of symmetry should be color-coded Color B and the other two vertices of the dart should be color-coded Color A. Notice the color of the kite and dart's vertices below (Wikipedia).
The rule for piecing the kites and darts together is the same color vertices have to touch. In other words, Color A must touch Color A and Color B must touch Color b. For example, this formation would be possible for a second Penrose tiling to occur (Wan, 2020).
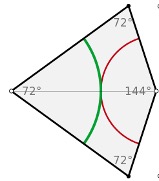
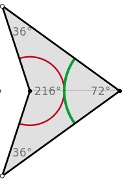
Notice how the white vertex of the kite overlapped the white vertex of the dart and how the black vertex of the kite overlapped the black vertex of the dart. This would be a viable Penrose tiling combination. Another way to approach the matching rules for the second Penrose tiling is by observing the drawn arcs within the kites and darts. As seen below, there are two arcs of different colors within both the kite and dart (Wikipedia).
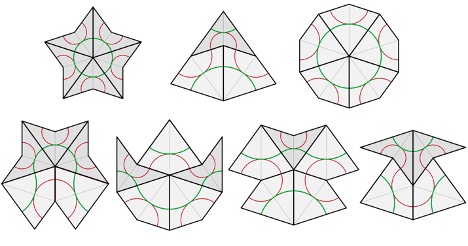
In order for it to be a viable Penrose tiling combination, the end of one green arc must seamlessly connect to another green arc and the same applies to the red arc. If the green arcs connect, the red arcs do not necessarily have to touch, but if they do, then it must be seamlessly. The same applies if the red arcs are connected, but the green arcs may or may not be. Below are the seven possible combinations of kites and darts for the second Penrose tiling (Wikipedia).
Previous Section: First Penrose Tiling/Original Pentagonal Tiling (P1)