Privacy and Social Network
Part 1. Introduction and History of Privacy and Social Network
Network theory is the study of graphs. Social network examines the structure of relationships between social entities like groups, websites or nation states. Since the 1970s, many of the mathematical and statistical tools used for studying networks. Social network analysis is the process of investigating social structures through network and graph theories. Since the 20th century, social scientists have used the concept of ‘social networks’ to imply the relationships of social systems from interpersonal to international. In the 1930s Jacob Moreno and Helen Jennings introduced basic analytical methods. In 1954, John Arundel Barnes started using the term systematically to denote patterns of ties. In fact, social network analysis has found applications in various academic disciplines. First of all, the network must be a subgraph of the original graph, in other words, its edges must come from the original graph. Second, it must span the original graph, which means it must include all the vertices of the original graph. Third, it need to be minimal, in other words, the total weight of the network should be as small as possible. A network is just another name for a connected graph. A network with no circuits is called a tree. A spanning tree of a network is a subgraph that connected all the vertices of the network and has no circuits. Among all spanning trees of a weight network, one with least total weight is called a minimum spanning tree of the network. In a tree, there is one and only one path joining any two vertices. Every edge is a bridge in a tree, and the tree has N vertices has N-1 edges. The reverse is also true.
Part.2 Minimum Spanning Tree (MST)
Definition A minimum spanning tree (MST) is a spanning tree of an edge-weighted graph that the sum of the weights of its edges is no larger than the weight of any other spanning tree. It is the base of both privacy and social network which is helpful in finding the cheapest and fastest network.
Properties
1. The graph is connected with n-1 edges in an n-vertex graph and is acyclic.
2. Removing an edge breaks the tree into two separate parts.
3. Adding an edge that connects two vertices in a tree creates a unique cycle.
4. The MST need not be unique. However, if all the edge weights in G are distinct, then G has a unique MST.
5. If the weights are positive, then a minimum spanning tree is in fact a minimum-weight subgraph connecting all vertices
Example Graph G. Suppose T is the MST for G where a is in G but not in T.
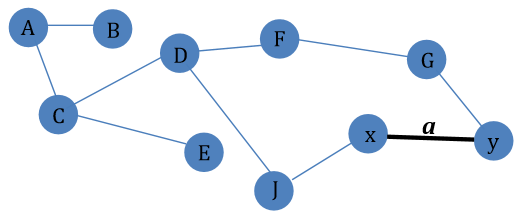
Proposition 1
Let G = (V, E, W) be a weighted graph and T = (V,S) be an MST for G, and let a=xy be an edge of G not in T. Then
a)w(a) >= w(k) for any edge k on the path in T from x to y.
b)If w(a) = w(k), then we may obtain another MST T’ for G by replacing k by a in S.
Proof. Consider a spanning tree T of the graph G, and let a be an edge of G but not of T. Then we may substitute k for a to retain a spanning tree. Hence, if we replace k by a in T, we obtain a spanning tree T’ of cost w(T’) = w(T) + w(a) - w(k) . If w(a) < w(k), then w(T’) < w(T). It is conflict to our assumption that T is a MST. If w(a) = w(k), then w(T’) = w(T). Therefore we know that T’ is also an MST.
Proposition 2
Let be a connected graph with distinct edge weights. Then there is a unique minimum spanning tree.
Proof. Suppose we have a minimum spanning tree T of the graph G and a different minimum spanning tree T’. W (e) is the weight of edge e and W (e’) is the weight of edge e’.
If W (e) > W (e’), then T is not a minimal spanning tree. If W (e) < W (e’), then T’ is not a minimal spanning tree. If we want both T and T’ to be the different minimal spanning tree, then we should have W (e) = W (e’). However, G is a connected graph with distinct edge weights, thus W (e) = W (e’) is impossible. As W (e) is not equal to W (e’), T and T’ should be the same.
Applications
1. Telecommunication networks. A business with several offices that need to lease phone lines to connect them up with each other, where the total costs should be minimized.
2. Transportation networks. To find the shortest path that visits each point at least once. It will be a Hamilton path if visits each point and edges only once. Note that we can always drop some edges to get a tree if visiting some points more than once, and thus in general the minimum spanning tree has a weight less than the original network.
3. Computer networks. The Internet is connected in a tree shape while we are using the searching engine. It is quite important to take advantage of the minimal spanning tree in order to find the information in the fastest and cheapest way.
4. Electrical Grid. An electrical grid is an interconnected network for delivering electricity from suppliers to consumers. The distribution of electricity and transmission is in tree shapes while the cheapest and simplest design is a question based on minimum spanning tree.

