Contents
[hide]Privacy and Social Network
By Group F
Part 1. Introduction and History of Privacy and Social Network
Network theory is the study of graphs. Social network examines the structure of relationships between social entities like groups, websites or nation states. Since the 1970s, many of the mathematical and statistical tools used for studying networks. Social network analysis is the process of investigating social structures through network and graph theories. Since the 20th century, social scientists have used the concept of ‘social networks’ to imply the relationships of social systems from interpersonal to international. In the 1930s Jacob Moreno and Helen Jennings introduced basic analytical methods. In 1954, John Arundel Barnes started using the term systematically to denote patterns of ties. In fact, social network analysis has found applications in various academic disciplines.
First of all, the network must be a subgraph of the original graph. In other words, its edges must come from the original graph. Secondly, it must span the original graph, which means it must include all the vertices of the original graph. Thirdly, it need to be minimal. In other words, the total weight of the network should be as small as possible. A network is just another name for a connected graph. A network with no circuits is called a tree. A spanning tree of a network is a subgraph that connected all the vertices of the network and has no circuits. Among all spanning trees of a weight network, one with least total weight is called a minimum spanning tree of the network. In a tree, there is one and only one path joining any two vertices. Every edge is a bridge in a tree, and the tree has N vertices has N-1 edges. The reverse is also true.
Part.2 Minimum Spanning Tree (MST)
Definition A minimum spanning tree (MST) is a spanning tree of an edge-weighted graph that the sum of the weights of its edges is no larger than the weight of any other spanning tree. It is the base of both privacy and social network which is helpful in finding the cheapest and fastest network.
Properties
1. The graph is connected with n-1 edges in an n-vertex graph and is acyclic.
2. Removing an edge breaks the tree into two separate parts.
3. Adding an edge that connects two vertices in a tree creates a unique cycle.
4. The MST need not be unique. However, if all the edge weights in G are distinct, then G has a unique MST.
5. If the weights are positive, then a minimum spanning tree is in fact a minimum-weight subgraph connecting all vertices.
Example Graph G. Suppose T is the MST for G where a is in G but not in T.
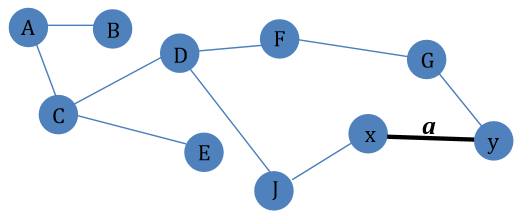
Proposition 1 Let G = (V, E, W) be a weighted graph and T = (V,S) be an MST for G, and let a=xy be an edge of G not in T. Then a)w(a) >= w(k) for any edge k on the path in T from x to y. b)If w(a) = w(k), then we may obtain another MST T’ for G by replacing k by a in S.
Proof. Consider a spanning tree T of the graph G, and let a be an edge of G but not of T. Then we may substitute k for a to retain a spanning tree. Hence, if we replace k by a in T, we obtain a spanning tree T’ of cost w(T’) = w(T) + w(a) - w(k) . If w(a) < w(k), then w(T’) < w(T). It is conflict to our assumption that T is a MST. If w(a) = w(k), then w(T’) = w(T). Therefore we know that T’ is also an MST.

Proposition 2 Let be a connected graph with distinct edge weights. Then there is a unique minimum spanning tree.
Proof. Suppose we have a minimum spanning tree T of the graph G and a different minimum spanning tree T’. W (e) is the weight of edge e and W (e’) is the weight of edge e’.
If W (e) > W (e’), then T is not a minimal spanning tree.
If W (e) < W (e’), then T’ is not a minimal spanning tree.
If we want both T and T’ to be the different minimal spanning tree, then we should have W (e) = W (e’).
However, G is a connected graph with distinct edge weights, thus W (e) = W (e’) is impossible.
As W (e) ≠ W (e’), T and T’ should be the same.
Applications
1. Telecommunication networks. A business with several offices that need to lease phone lines to connect them up with each other, where the total costs should be minimized.
2. Transportation networks. To find the shortest path that visits each point at least once. It will be a Hamilton path if visits each point and edges only once. Note that we can always drop some edges to get a tree if visiting some points more than once, and thus in general the minimum spanning tree has a weight less than the original network.
3. Computer networks. The Internet is connected in a tree shape while we are using the searching engine. It is quite important to take advantage of the minimal spanning tree in order to find the information in the fastest and cheapest way.
4. Electrical Grid. An electrical grid is an interconnected network for delivering electricity from suppliers to consumers. The distribution of electricity and transmission is in tree shapes while the cheapest and simplest design is a question based on minimum spanning tree.
Part.3 Privacy
Definition Privacy can be translated into different meanings, depending on the context. From the political standpoint, Schement and Curtis (1995) describe privacy as security against intrusion by government. In general, privacy can be described as the ability of an individual or group to seclude themselves or information about themselves and thereby reveal themselves selectively (Yves Le Roux).
Issues
With the development of technology and the existence of social media, it is getting harder and harder for people to keep their privacy. Any information that we uploaded into our social media can be accessed by hundreds of people through the network, even if we did not intend to do that. Not only information that we purposely uploaded to our social media, the information about the things that we browsed on our web browser on our free time is also being watched and collected, so that the ad makers can tailored the kinds of advertisements that shows on the web pages that we visited so that it relates to us in order to increase the chance of us clicking the link.
Other than our web browser history, our personal information are also in danger of exposure through social medias. An analysis of personal online journals revealed that personal informations such as name, address, birth date, location, and e-mail addresses are revealed to third parties online. The amount of informations revealed could result to cyberstalking and identity theft. Shortly, it is unavoidable to say that the amount of social media exposure creates danger to our privacy.
Privacy Paradox
Definition On May 2015, Benjamin Wittes and Jodie C. Liu wrote a paper titled “The Privacy Paradox: The privacy benefits of privacy threats”. The main idea is that “most technologies often enhance and diminish privacy, depending on how it is used, who is using it, and what sorts of privacy that person values. Individual concern with privacy often will not involve privacy in the abstract, but rather vis a vis specific audiences - that is to say that the question of privacy from who matters. At least some modern technologies that we commonly think of as privacy-eroding may in fact enhance privacy from the people in our immediate surrounding.”
One hand, we are sharing our thoughts and information about us online, and on the other hand, government agencies and marketers are collecting personal data about us. Katz and Rice (2002) describe the Internet as a panopticon, which is a “constant view of individuals through para societal mechanisms that influence behavior simply because of the possibility of being observed.”
Part.4 Social Network
Definition A social network is a social structure that made up of a set of nodes (individuals or organizations) connected by edges (relationships). It is usually represented as a graph. We can learn the interactions between people by studying their social web.
Graphs
A graph is a set of nodes and a set of links.
We represent a network by a graph (N,g), which consists a set of nodes N = {1, 2, 3, … , n} and an n x n matrix g = [gij]i,j ∈N. The matrix is called an adjacency matrix, where gij ∈{0,1} represents the connection of an edge from node i to node j.
Types of graphs
❖Weighted Graphs The edge element g_ij > 0
❖Directed Graphs g_ij ≠g_ji for i, j ∈N. Edges are bidirectional.
❖Undirected Graphs g_ij = g_ji for i, j ∈N. All edges are directed from one vertex to another.
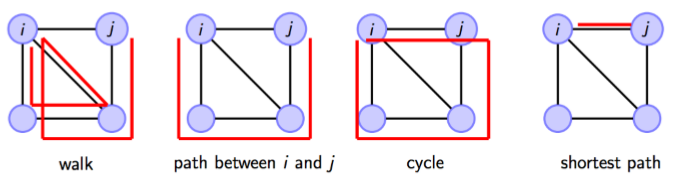
Walks, Paths and Cycles
❖ Walks - a sequence of edges.
❖ Paths - a sequence of edges between nodes i and j, a walk with no repeated edges.
❖ Cycles - a path where the final edge connects to the initial node.
❖ Shortest Path (Geodesic) - the path with minimum number of edges connecting 2 nodes.
Properties of Networks
It is fairly easy to analyze the graph visually if we have a small network but it gets complicated when we come with a large network. In order to solve this we come up with summary statistics and performance metrics to describe and compare networks.
❖ Diameter and mean path length
❖ Centrality
❖ Degree distributions
1. Diameter and mean path length
Let l(i,j) denotes the length of shortest path between node i and node j. Then the diameter of the graph is the largest distance between any 2 nodes, which can be denoted as diameter = Max l(i,j).
The mean path length is the average distance between any 2 nodes.
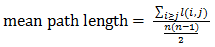
2. Centrality
❖ Degree - number of edges a given node has.
❖ Closeness - how close is a given node to any other nodes.
❖ Betweenness - number of times which any node needs a specific node to reach any other nodes by the shortest path.
3. Degree Distributions
Degree distributions is a relative frequency distribution of nodes that have different degrees. It is a probability distribution and is denoted by P(d).
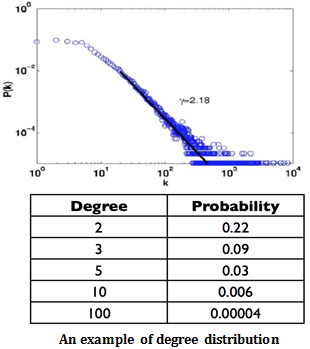
Definition Rough idea of friendship paradox is that your friends on social media have more friends than you have on average first discovered by Scott L. Field. More specifically, it is highly likely for a person with large amount of friends to be seen among mutual friends list. It can be supported by sampling bias. Intuitively, people that have many friends tend to be your friend in the first place.
Mathematical Backgrounds
These paradox is related to arithmetic geometric mean equality and Cauchy-Schwarz inequality. However, we will focus on the concepts related to graph. Assume social network is represented as an undirected graph G = (V,E). Set V which is consisted of vertices is the number of people in a social network. E is the edge which means that if an edge exists, they are friends. We can induce from it that friend is symmetric relationship; if x is friend of y, then y is friend of x, especially in a social network. Field consider the average of degrees of vertices are average number of a person’s friends. If vetex v communicates with n = degrees(V), then that can be explained as below.
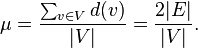
To compare it with another person, you can square d(v) which can be explained as pairs of friends of two people.
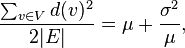
Since mu and alpha are greater than zero, we can say the value - mu is also greater than zero. That means chosen friend of yours to compare has more friends in average than yours.
Applications
This is analysis about mutual friends of others. Therefore, it can be applied to the field once two random vertices are communicated, how much would it be spreaded. The perfect situation of it is epidemics. By using this knowledge, it will be helpful to forecast how fast and much a disease would be spreaded away. Also we can always be more cautious once some disease occurs in any random places by any random people. The people one would touch will greater than we think and that leads to growth of spread exceptionally high.
References
Freeman, L. C. (2004). The development of social network analysis: a study in the sociology of science. Vancouver, B. C.: Empirical Press.
A Theorem on the Uniqueness of Minimum Spanning Tree. 234247 Algorithms 1, Retrieved Winter 2004/5.
ICS 161: Design and Analysis of Algorithms: https://www.ics.uci.edu/~eppstein/161/960206.html
Minimum Spanning Trees: http://algs4.cs.princeton.edu/43mst/
Minimal Spanning Tree: http://homepages.math.uic.edu/~leon/cs-mcs401-s08/handouts/mst.pdf
Electrical Grid: https://en.wikipedia.org/wiki/Electrical_grid
Minimum Spanning Tree Property 3 and 4: Unique Edge Weights: https://www.youtube.com/watch?v=Ftkv1Ijp5Jw
CS104 - Social Networks and Graph Theories: http://pc57724.uni-regensburg.de/morgan/teaching/CS104-Social_Networking.pdf
Graph Theories and Social Networks:http://economics.mit.edu/files/4620
Undirected Graphs:http://mathinsight.org/definition/undirected_graph
Directed Graphs: http://mathinsight.org/definition/directed_graph
Theorems related to networking : https://en.wikipedia.org/wiki/Network_theory
Social networking analysis. https://en.wikipedia.org/wiki/Social_network_analysis
Friendship paradox: https://en.wikipedia.org/wiki/Friendship_paradox
Minimum Spanning Tree: https://en.wikipedia.org/wiki/Minimum_spanning_tree
Network Theorem: https://en.wikipedia.org/wiki/List_of_network_theory_topics
Wittes. B & Liu.J (May 21, 2015). The privacy paradox: The privacy benefits of privacy threats. http://www.brookings.edu/research/papers/2015/05/21-privacy-paradox-wittes-liu
Susan B. Barnes (September 4, 2006). A Privacy Paradox: Social Networking in the United States. Volume 11, Number 9

