Parzen Windows - Rhea

Post your slecture material here. Guidelines:

• If you are making a text slecture
  • Type text using wikitext markup languages
  • Type all equations using latex code between <math> </math> tags.
  • You may include links to other Project Rhea pages.

Introduction

As a Local Density Estimation method, Parzen Windows, focuses on estimating the density in a small region and making a decision based on that specific region. The density estimation relies on the specific test point being classified and the region around it. The reasoning behind it is to not focus on the accuracy of density estimation, but on the accuracy of decision making.

The idea is to create a smaller region, with the test point at its center, within the full region of the training data, and estimate the density in that small region and classify that test point based on the class with the highest density.

The method relies on the type or shape of the window used to form the smaller region.

Parzen Windows Method with a Cube Window

As mentioned before the reasoning behind it is to accurately make decisions and classify data. Thus the ideal method to explain how it works is to start with the classification process.

Given a set of training data in a region $ \Re^n $, and a point $ x_0 $ in the region $ \Re^n $.

a unit cube region $ R $ is created around $ x_0 $

using the following window function to count the samples in $ R $.

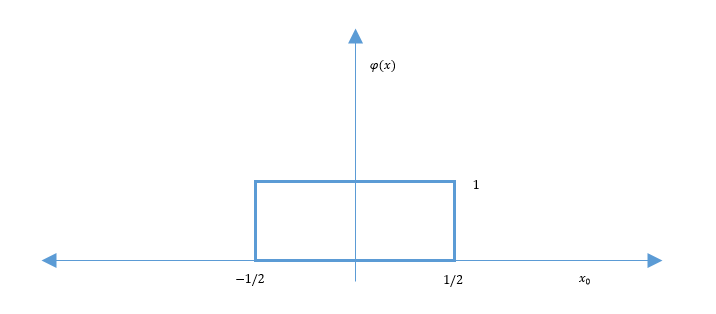
$ \phi(x) = \rho(x_1,x_2,...,x_n) = \begin{cases} 1 \quad if \left\vert x_1 \right\vert < \frac{1}{2}, \left\vert x_2 \right\vert < \frac{1}{2},..., \left\vert x_n \right\vert < \frac{1}{2} \\ 0 \quad else \\ \end{cases} $

Which yields the figure bellow.

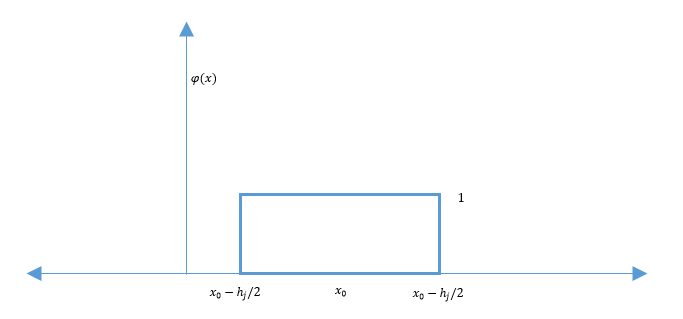
As we can see in the figure above, the window is not centered the point. To fix that issue we simply shift the window to be centered at $ x_0 $. Doing that would allow us to count the training data around the mean $ x_0 $.

$ \phi(x - x_0) = \begin{cases} 1 \quad if x \in R \\ 0 \quad else \\ \end{cases} $

So the number of training points inside $ R $ is defined by:

$ R = \sum_{l=1}^N \phi(x_l - x_0) $

$ \Rightarrow \widehat{\rho}(x_0) = \frac{1}{N} \frac{\sum_{l=1}^N \phi(x_l - x_0)}{\int_{\Re^n} \phi(x)\, dx} $

$ \Rightarrow \widehat{\rho_i}(x_0) = \frac{K_j}{j V_j} = \frac{1}{j V_j} \sum_{l=1}^j \phi(\frac{x_l - x_0}{h_j}) $

$ K_j = $ The number of training points in $ \{x_1,x_2,...,x_j\} $ inside $ R_j $

$ R_j = $ The region defined by $ \phi(\frac{x_l - x_0}{h_j}) $

$ V_j = $ The volume of $ R_j $

$ V_j = \int_{\Re^n} \phi(\frac{x}{h_j})\, dx $

Thus leading to:

After shifting the window it is now centered at $ x_0 $ and the $ \rho_i(x_0) $ would be the density estimate in that region for the class i. After applying the $ \rho_i(x_0) $ function on all the classes, we choose the class with the highest number density for $ x_0 $.

We can think of

$ /frac{1}[V_j} \phi(\frac{x_l - x_0}{h_j}) = \delta_j(x_j - x_0) \longrightarrow \delta(x - x_0) $

As an approximation of a unit impulse centered at $ x_0 $

$ \delta(x) = \begin{cases} \infty \quad if x = 0 \\ 0 \quad else \\ \end{cases} $

$ \int \delta(x)\, dx = 1 $

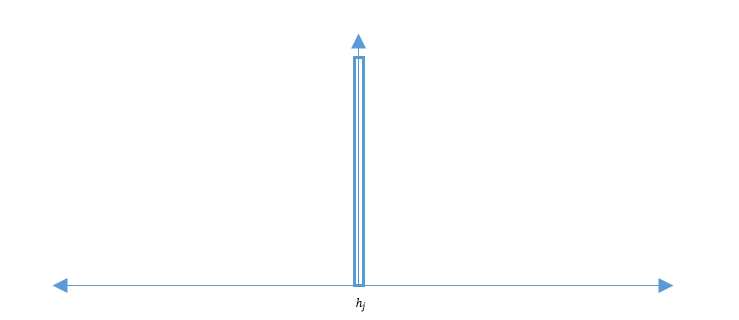
So as $ h_j \rightarrow 0 $ it will look like:

So the smaller $ h_j $ get the lower the number of training point that fall inside the window.

The Parzen Windows Method in General

We can pick any function $ \phi: \Re^n \rightarrow \Re \geqslant 0 $

such that

$ \lim_{h_j \to 0}\frac{1}{\int_{\Re^n} \phi(\frac{x}{h_j})\, dx} \phi\left (\frac{x}{h_j})\rightarrow \delta(x)\right ) $

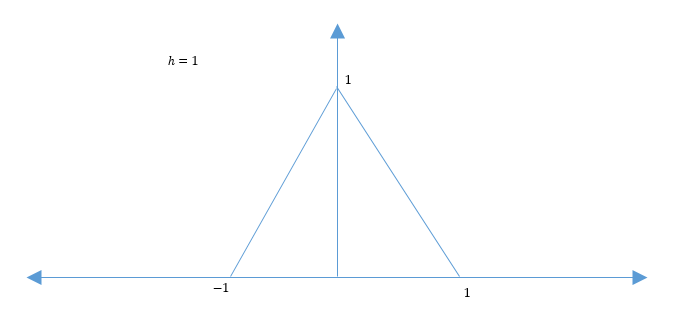$ \phi(x) = \begin{cases} 1 - x \quad if 0 \leqslant x \leqslant 1 \\ 1 + x \quad if -1 \leqslant x \leqslant 0 \\ 0 \qquad\quad else \end{cases} $

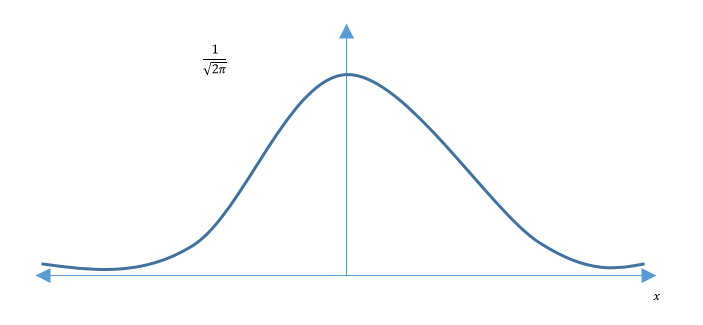$ \phi(x) = \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}} $

$ \widehat{\rho}(x_0) = \frac{1}{N} \frac{1}{\int \phi(\frac{x_l - x_0}{h})\, dx} \sum_{l=1}^N \phi(\frac{x_l - x_0}{h}) $

Parameterized by h and the $ \phi $ function.

The main issues faced are:

• Bad estimates when no points exist in a region
• High computational cost

This works because instead of estimating

$ P = \int_{R} \rho(x)\, dx \rightarrow \rho(x_0) $

we now consider

$ P_\phi = \int_{\Re^n} \rho(x) \frac{\phi \left ( \frac{x - x_0}{h} \right )}{\int \phi(\frac{x}{h})\, dx}\, dx $

$ \quad = \rho(x) * \frac{\phi(\frac{x}{h})}{Vol(\phi)} \bigg|_{x = x_0} \xrightarrow[h \rightarrow 0]{} \rho(x) * \delta(x)\bigg|_{x = x_0} = \rho(x) $

Assuming $ \rho(x), \phi(x) $ continuous mean $ x_0 $.

Look at the convergence of $ \widehat{\rho_j}(x_0) $ in "mean square", i.e.

$ \lim_{j \to \infty} E(\widehat{\rho_j}(x_0)) = \rho(x_0) $

and

$ \lim_{j \to \infty} Var(\widehat{\rho_j}(x_0)) = 0 $

we have

$ \widehat{\rho_j}(x_0) = \frac{1}{j V_j} \phi(\frac{x_l - x_0}{h_j}), where V_j = \int \phi(\frac{x}{h_j})\, dx $

$ \implies E(\widehat{\rho_j}(x_0)) = \frac{1}{j} \sum_{l=1}^j E(\frac{1}{V_j} \phi(\frac{x_l - x_0}{h_j})) $

Questions and comments

If you have any questions, comments, etc. please post them on this page.

Back to ECE662, Spring 2014