Curse of Dimensionality - Rhea

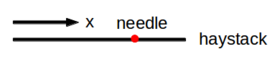
Needle in a haystack

You lost your needle in a haystack. If the world you live in has just one dimension, then you are lucky because the haystack is a line segment. Finding the needle only requires you to start from one end of the segment, heading towards the other end until hitting the needle:

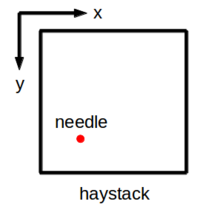
Not bad, right? If you are a 2D creature, a needle in a haystack now becomes a small trouble because it can be any point in a square:

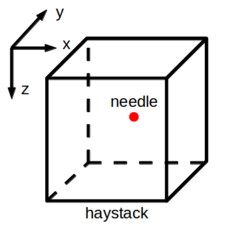
There is much more space for the possible location: within the haystack, the needle can move along either the $ x $-axis or the $ y $-axis. Things get worse and worse as the number of dimensions grows. You can't imagine how alien high-dimensional creatures would look for something missing in their world because even in three dimensions, this task turns out to be frustrating (from everyday life experience):

The difficulty of finding the needle starting from a certain point in a high-dimensional haystack implies an import fact: the points tend to distribute more sparsely (i.e., they are more dissimilar to each other) in high-dimensional space, since the Euclidean distance between two points is large as long as they are far apart in the direction of at least one dimension, even though they may be quite close in the direction of all the other dimensions. This fact can be further illustrated quantitatively by the following example. In $ N $-dimensional space, suppose we want to count all the neighbors around a certain point within a hypercube with the edge length equal to 1. We also consider a bigger hypercude around the point with the edge length equal to $ 1+\epsilon $.

Questions and comments

If you have any questions, comments, etc. please post them on this page.

Back to ECE662, Spring 2014