Student summary Filtering - Rhea

PAGE UNDER CONSTRUCTION

Filtering

Introduction

Filtering in a broad sense, is a method of removing any unwanted quantity from a mixture of the desired quantity and the undesired quantity. In the world of signals, this generally applies to the process of either separating different channels of a signal, or removing a noise signal to get the original signal.

This usually makes more sense when we talk about something real. Say, music, or images, or surprisingly, even the stock market! That's right. It is possible, from simple spectral analysis to "filter" out long-term and short term trends from any time varying data. This includes weather, astronomical events, and pretty much any time-varying signal you can think of.

Simple Example

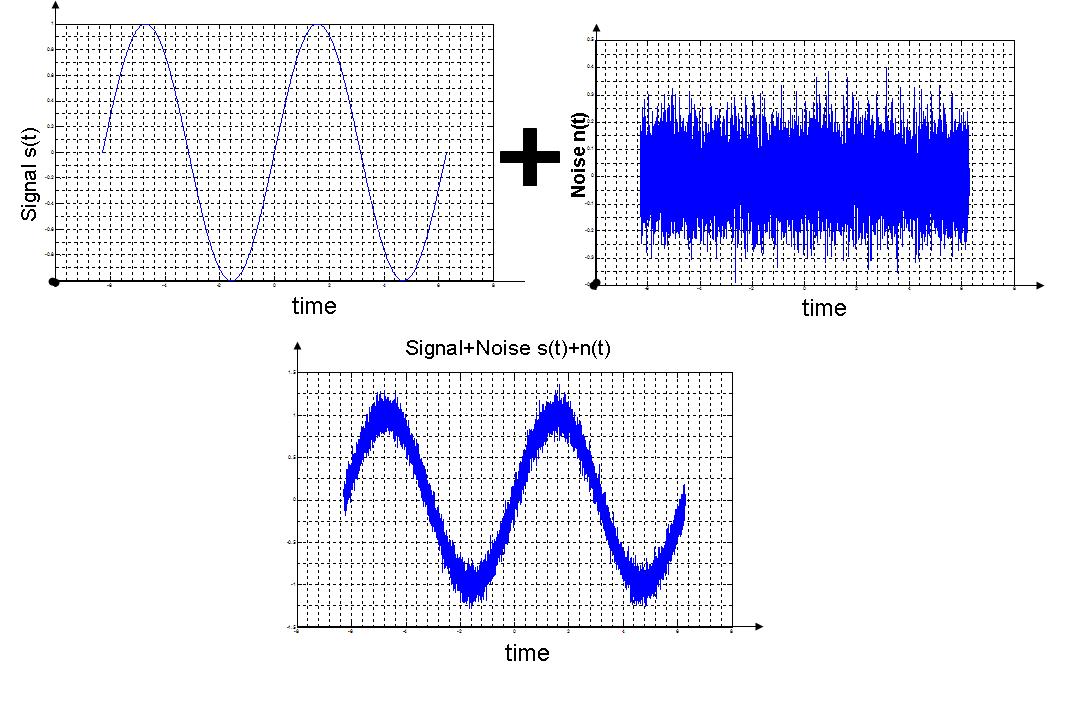
I always like to start out with our friendly sine wave. After all, that is what Fourier started with too.
So, what we do is start by taking a clean sine wave from -2pi to 2pi
To the sine wave, we add some pretty ugly Gaussian noise, shown above.
What results is a much noisier signal, as can be clearly seen.

To try this yourself, you can plop the following in an m-file

clear all;
close all;

clc;

t = [-2*pi:.1:2*pi];
signal = sin(t);
plot(t,sin(t));
grid minor;

noise = randn(1,length(t));
noise = noise/10;
figure;
plot(t,noise);
grid minor;

mixed = noise + signal;
figure;
plot(t,mixed)
grid minor;

Now if someone presented us an ugly signal like that, we can without panicking, get the original signal back
How? LOW PASS FILTER
However, a Low Pass Filter isn't a magic device that removes noise
It needs to have well defined cut off frequencies and pass-band gains.

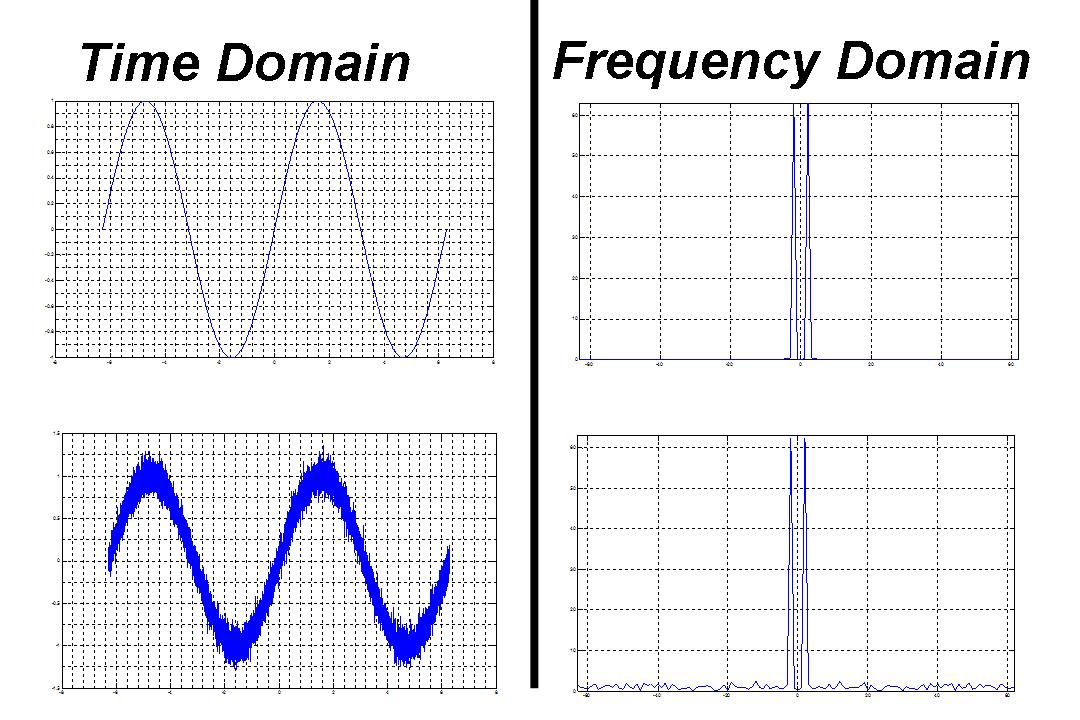
To understand this better, let us see how our signals look in the frequency domain
To do this, we take the original signal's FFT (this will be an N point FFT where N = 126 because we have an interval of -2pi or -6.283 to 2 pi or 6.283 at intervals of .1, Hence 126 samples and we know that N samples will yield N points in the FFT)
An important thing to remember is that the frequency corresponding to the kth sample is actually $$ 2pik/N $$

To try these figures, you may use the following code in continuation with the previous code above:

k = -63:62;

figure;
plot(k,fftshift(abs(fft(signal))));
grid;
axis([min(k),max(k),0,63]);

figure;
plot(k,fftshift(abs(fft(mixed))));
grid;
axis([min(k),max(k),0,63]);

The first thing to note from the figure is that the signal with no noise has a frequency spectrum like we expected, two nice clean impulses corresponding to it's natural frequency.
On the other hand, the spectrum of the sin wave with added noise, has a good deal of frequency components outside the natural frequency, and since the noise we added was Gaussian instead of a single frequency, it's all over the spectrum.
To remove the noise, we need to remove the frequency components that correspond to it in the Fourier Domain
The problem however is, that since the noise affects all regions of the spectrum, removing it's frequency components, or conversely preserving the original signal's components, will not remove the noise completely.
Still, let's see the best that can be done.

Low Pass Filter

Again, the objective is to design a low pass filter that keeps the frequency components of the original signal and kills everything else.
To visualize this, think of multiplying a box

$H(\omega) = \left\{ \begin{array}{c l} A &\omega \in [-w_0,w_0]\\ 0 & \omega\not\in [-w_0,w_0] \end{array} \right.$

with the frequency domain of the signal to be filtered, so that what results (ideally) is

$X(\omega) = \left\{ \begin{array}{c l} AX(\omega) &\omega \in [-w_0,w_0]\\ 0 & \omega\not\in [-w_0,w_0] \end{array} \right.$

Of course, filters are not ideal in the real world, and instead of a constant A in the pass-band, we get a reasonably constant function of w in the pass band and a severely attenuated $\epsilon$ as the gain for the stop band, where $\epsilon ->0$

Filters in MATLAB

So, let's see how good we can make our filters, so that they meet the specifications above.
Our cut-off frequency in this case is 1/2*pi Hz because $\sin(2\pit)$