Student summary Filtering - Rhea

Filtering

Introduction

Filtering in a broad sense, is a method of removing any unwanted quantity from a mixture of the desired quantity and the undesired quantity. In the world of signals, this generally applies to the process of either separating different channels of a signal, or removing a noise signal to get the original signal.

This usually makes more sense when we talk about something real. Say, music, or images, or surprisingly, even the stock market! That's right. It is possible, from simple spectral analysis to "filter" out long-term and short term trends from any time varying data. This includes weather, astronomical events, and pretty much any time-varying signal you can think of.

Simple Example

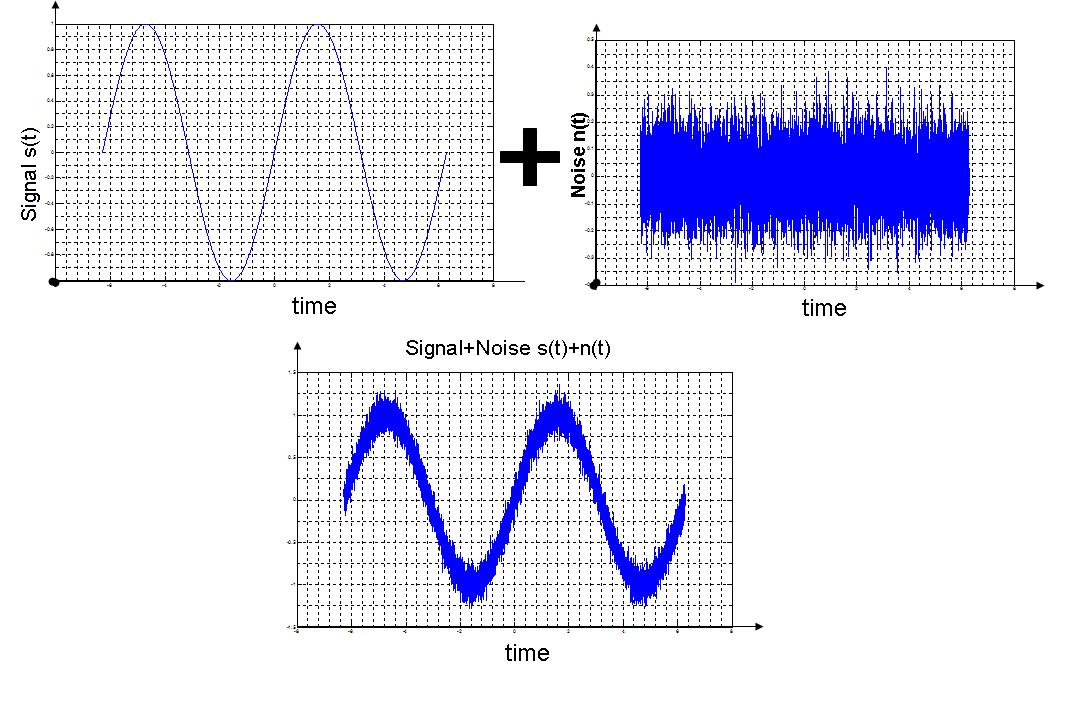
• I always like to start out with our friendly sine wave. After all, that is what Fourier started with too.
• So, what we do is start by taking a clean sine wave from -2pi to 2pi
• To the sine wave, we add some pretty ugly Gaussian noise, shown above.
• What results is a much noisier signal, as can be clearly seen.

To try this yourself, you can plop the following in an m-file

clear all;
close all;

clc;

t = [-2*pi:.001:2*pi];
signal = sin(t);
plot(t,sin(t));
grid minor;

noise = randn(1,length(t));
noise = noise/10;
figure;
plot(t,noise);
grid minor;

mixed = noise + signal;
figure;
plot(t,mixed)
grid minor;

• Now if someone presented us an ugly signal like that, we can without panicking, get the original signal back
• How? LOW PASS FILTER
• However, a Low Pass Filter isn't a magic device that removes noise
• It needs to have well defined cut off frequencies and pass-band gains.

• To understand this better, let us see how our signals look in the frequency domain
• To do this, we take the original signal's FFT (this will be an N point FFT where N = 12567 because we have an interval of -2pi or -6.283 to 2 pi or 6.283 at intervals of .001, Hence 12567 samples and we know that N samples will yield N points in the FFT)
• An important thing to remember is that the frequency corresponding to the kth sample is actually $ 2\pik/N $