Contents
[hide]Derivation of Fischer's Linear Discriminant
Main article: [Derivation of Fisher's Linear Discriminant]
The derivation was completed in this lecture.
Recall from last lecture
Last time, we considered
$ J(\vec{w}) = \frac{\vec{w}^t S_B \vec{w}}{\vec{w}^t S_W \vec{w}} $
which is explicit function of $ \vec{w} $
One can do this because numerator of $ J(\vec{w}) $ can be written as
$ \mid \tilde m_1 - \tilde m_2 \mid^2 = \mid w \cdot (m_1 - m_2) \mid^2 = w^t (m_1 - m_2) (m_1^t - m_2^t) w $
$ \rightarrow S_B = (m_1 - m_2) (m_1^t - m_2^t) $
In a same way, denominator can be written as
$ \tilde s_1^2 + \tilde s_2^2 = \sum_{y_i \in class \ i} (w \cdot y_i - \tilde m_1)^2 = \sum w^t (y_i - m_i)(y_i^t - m_i^t) w $
$ = w^t \left[ \sum (y_i - m_i)(y_i^t - m_i^t) \right] w $
$ \rightarrow S_W = \sum_{y_i \in class \ i} (y_i - m_i)(y_i^t - m_i^t) $
Fisher Linear Discriminant
It is a known result that J is maximum at $ \omega_0 $ such that $ S_B\omega_0=\lambda S_W\omega_0 $. This is the "Generalized eigenvalue problem.
Note that if $ |S_W|\neq 0 $, then $ {S_W}^{-1}S_B\omega_0=\lambda\omega_0 $. It can be written as the "Standard eigenvalue problem". The only difficulty (which is a big difficulty when the feature space dimension is large) is that matrix inversion is very unstable.
Observe that $ S_B\omega_0=(\vec{m_1}-\vec{m_2})(\vec{m_1}-\vec{m_2})^T\omega_0=cst.(\vec{m_1}-\vec{m_2}) $. Therefore the standard eigenvalue problem as presented above becomes $ {S_W}^{-1}cst.(\vec{m_1}-\vec{m_2})=\lambda\omega_0 $. From this equation, value of $ \omega_0 $ can easily be obtained, as $ \omega_0={S_W}^{-1}(\vec{m_1}-\vec{m_2}) $ or any constant multiple of this. Note that magnitude of $ \omega_0 $ is not important, the direction it represents is important.
Fischer's Linear Discriminant in Projected Coordinates
- Claim**
$ \vec{c}=\omega_0={S_W}^{-1}(\vec{m_1}-\vec{m_2}) $
is the solution to $ \mathbf{Y}\vec{c}=\vec{b} $ with $ \vec{b}=(d/d_1, \cdots, <d_1 times>, d/(d-d_1), \cdots, <(d-d_1) times>)^T $
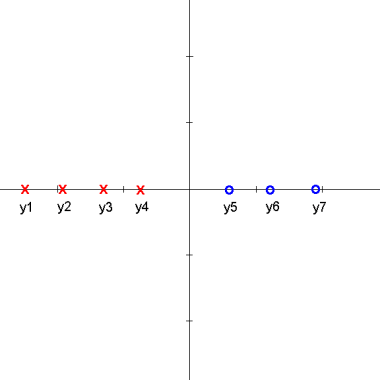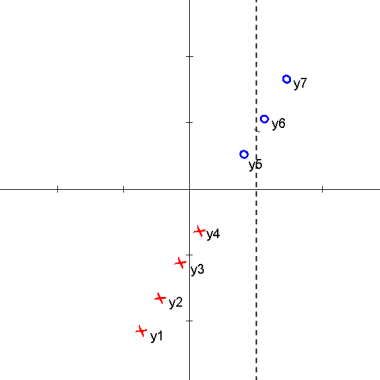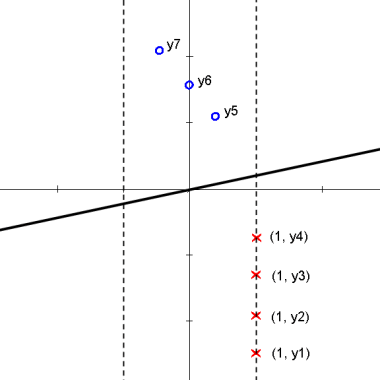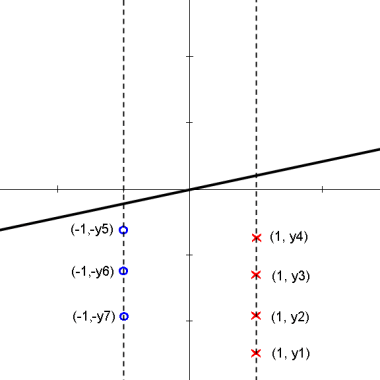
Here is an animation of the 1D example given in class on projections
Explanation *(feel free to change / correct)*
starts with $ \vec{\omega} \bullet y_i + \omega_0 > 0 $ for class 1 and $ \vec{\omega} \bullet y_i + \omega_0 < 0 $ for class 2
the data points are then projected onto an axis at 1 which results in
$ \vec{\omega} \bullet y_i > 0 $ for class 1 and $ \vec{\omega} \bullet y_i < 0 $ for class 2
one class is then projected onto an axis at -1 which results in
$ \vec{\omega} \bullet y_i > 0 $ for all $ y_i $
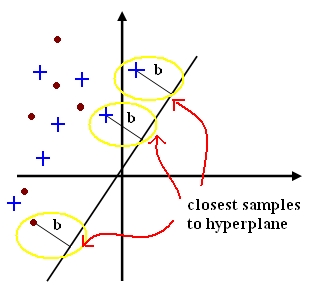
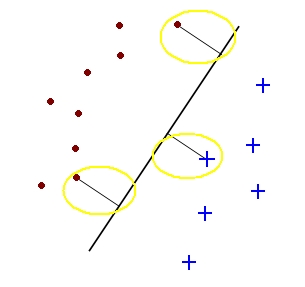
Support Vector Machines (SVM)
A support vector for a hyperplane (vector c) with margin (bi >= b) is a sample (yio) such that (*yio = b.) (someone please fix with mathtype)
Support Vector Machines are a two step process:
1) Preprocessing - X1,...,Xd features in kth dimensional real space is mapped to features in n dimensional real space where n>>k.
2) Linear Classifier - separates classes in n dimensional real space via hyperplane. - Support Vectors - for finding the hyperplane with the biggest margins. - Kernel - to simplify computation (This is key for real world applications)