Contents
Homework 7, ECE438, Fall 2015, Prof. Boutin
Hard copy due in class, Wednesday October 14, 2015.
Questions 1
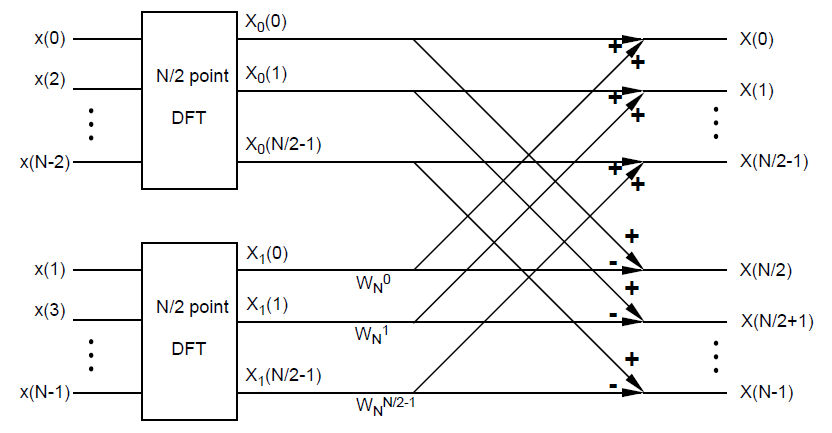
Draw the complete flow diagram for the "decimation by two" FFT algorithm to compute a 122 point DFT. How many complex operations does your algorithm take? How many operations would this DFT computation take if you were using the summation formula (i.e., the definition of the DFT) instead?
Solution
Diagram of "decimation by two" FFT computing N-pt DFT. N=122 in this question.
where $ W_N^k = e^{-j2\pi k/N} $
A direct computation of DFT requires $ N^2 = 14884 $ times of complex multiplications and $ N^2-N = 14762 $ times of complex additions.
Using "decimation by two" FFT algorithm, the total number of multiplications is $ 2\cdot (\frac{N}{2})^2 + \frac{N}{2} = 7503 $ and the total number of additions is $ 2((\frac{N}{2})^2-\frac{N}{2}) + N = 7442 $
Questions 2
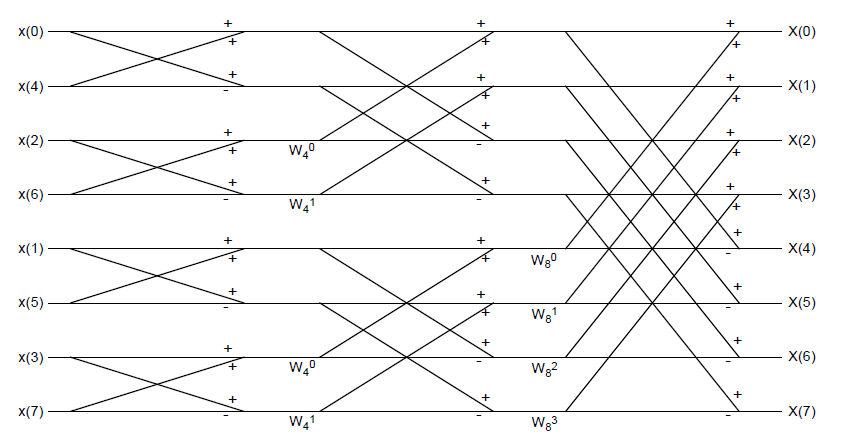
Draw a complete flow diagram for of the "radix-2" FFT algorithm to compute an 8 point DFT. How many complex operations does your algorithm take?
Solution
Diagram of "radix-2" FFT computing 8-pt DFT.
where $ W_N^k = e^{-j2\pi k/N} $
Recall the definition of DFT:
$ X[k]=\sum_{n=0}^{N-1} x[n]e^{-j2\pi k/N},\ k=0,...,N-1 $
In this question N=8
If we use summation formula to compute DFT, for each k, we need N times complex multiplications and N-1 times complex additions.
In total, we need N*N=64 times of complex multiplications and N*(N-1)=56 times of complex additions.
In decimation-in-time FFT algorithm, we keep on decimating the number of points by 2 until we get 2 points DFT. At most, we can decimate $ v=log_2 N $ times. As a result, we get v levels of DFT. Except for the first level (2-pt FFT), which only needs N times complex additions, for the rest of levels, we need N/2 times of complex multiplications and N times of complex additions.
In total, we need $ \frac{N}{2}(log_2 N -1)=8 $ times of complex multiplications and $ Nlog_2 N=24 $ times of complex additions.
(Note: when $ N $ is large, $ log_2 N -1 \approx log_2 N $. So the number of multiplications becomes $ \frac{N}{2}log_2 N $.)
Question 3
Use the definition of the DFT (the summation formula) to obtain two different FFT algorithms to compute a 6 point DFT. Draw a flow diagram for each of your algorithms, and compute the total number of complex operations they would require. Compare these two numbers with the number of complex operations this computation would take if you were using the definition of the DFT instead.
Hand in a hard copy of your solutions. Pay attention to rigor!
Presentation Guidelines
- Write only on one side of the paper.
- Use a "clean" sheet of paper (e.g., not torn out of a spiral book).
- Staple the pages together.
- Include a cover page.
- Do not let your dog play with your homework.
Discussion
- Write question/comment here.
- answer will go here