ECE-QE-CE-4-2015 - Rhea

ECE Ph.D. Qualifying Exam
Computer Engineering, Question 04 (CE-4): Architecture
August 2015

I. Processor

In modern out-of-order processors pipelines, there are many "pipeline loops" due to data/information generated in later pipeline stages and used in earlier stages (e.g., register bypass, branch resolution, and rename table update). Modern pipelines have many such loops each of which is relevant only to a subset of instructions.

Assume single-issue pipeline for the following questions.

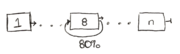
1. What is the increase in the cycles per instruction (CPI), if 80% of instructions incur a loop from the 8th stage to the 8th stage? Also, give a real example of such a loop.

Assuming each stage can be completed in one cycle: If 80% of instructions incur a one cycle/stage loop-back, this implies that stage would have to be performed again. Thus, a one cycle penalty for 80% instructions would result in a 1 * 0.8 = 0.8 CPI increase.

An example of such a loop may be found either in incrementers (i++) or decrementers (i--).

2. For a loop from the 15th stage back to the 1st stage, the pipeline employs prediction with accuracy 90% (you should figure out how prediction lessens the loops' impact on the CPI). What is the increase in the CPI if the loop is relevant to 20% of all instructions?

• For 20% of instructions, there is a pipeline loop from the 15th to the 1st stage.
• For 90% of such instructions, the pipeline can predict this behavior.

So 18% (0.2 * 0.9) of instructions loop from the 15th stage to the 1st stage in a predicted manner. This means that 2% (0.2 * 0.1) of instructions loop from the 15th stage to the 1st stage without prediction and must pay a penalty. This penalty is where the increase in CPI will originate. When a missprediction occurs, the penalty here is 15 stages/cycles which 2% of instructions must pay.

Therefore, 0.02 * 15 cycles/stages = 0.3 increase in CPI. If the correctly predicted loop back from the 15th to the 1st stage does not have to pay the penalty (I assume this here due to the nature of the correct prediction), then 0.3 is the total increase to the CPI.

3. For a loop from the 15th stage back to the 1st stage and another from the 10th stage back to the 5th stage, if 1% of instructions are affected by the former loop and 3% (including the previous 1%) are affected by the latter loop, what is the increase in CPI?

From the question we know that a loop back from the 15th to the 1st stage equates to a 15 cycle/stage penalty. A loop then from the 10th stage back to the 5th stage is a cycle/stage penalty (as stages 5, 6, 7, 8, 9, and 10 all have to be visited again).

Then we know that 1% of instructions pay the 15 stage/cycle penalty and 3% of instructions pay the 6 stage/cycle penalty.

The problem states that this 3% "includes the previous 1%." Given this, to calculate the affect of this loop separately, I assume the 3% is instead 2% (3%-1%).

Then:

• 1% pay the 15 stage penalty: 0.01 * 15 = 0.15
• 2% pay the 6 stage penalty: 0.02 * 6 = 0.12

Therefore, the total increase to the system CPI imposed by these two loop-backs is 0.27 CPI.

II. Memory systems

1. Assume 25% of all instructions are loads and stores, L1 miss rate is 20%, L2 miss rate is 20% (out of L1 misses), and L1, L2, main memory latencies are 3, 32, and 300 cycles, respectively, and their bandwidths are, respectively, 1 access (hit or miss) every 1, 8, and 30 cycles. What is the achievable IPC (instructions per cycle), if we assume abundant parallelism due to simultaneous multithreading?

The question says we can assume abundant parallelism due to simultaneous multithreading. For my solution, I take this to mean that when a memory component (L1, L2, or main memory) misses, other instructions can still use this memory unit (up until the memory unit's bandwidth cap has been reached).

• So since L1's latency is 3 cycles and it can do one access every 1 cycle, this means that it can handle 3 (3 / 1 ) overlapping operations at one time.
• L2's latency is 32 cycles and it can do one access every 8 cycles. This means that it can handle 4 (32 / 8 ) overlapping operations at one time.
• Main memory's (MM's) latency is 300 cycles and it can do one access every 30 cycles. This means that it can handle 10 (300 / 30) overlapping operations at one time.

We know average memory access time (AMAT) can be calculated: hit time + (miss rate * miss penalty). We can use this to help calculate the achievable IPC such as,

AMAT (in CPI) = (L1_hitTime + L1_missRate * L1_missPenalty) / L1_nOverlap,

where

L1_missPenalty = (L2_hitTime + L2_missRate * L2_missPenalty) / L2_nOverlap

and

L2_missPenalty = (MM_{hitTime) / MMnOverlap.}

Using the problem's parameters:

L2_missPenalty = 300 / 10 = 30.

L1_missPenalty = (32 + 0.2 * 30) / 4 = 9.5.

AMAT = (3 + 0.2 * 9.5) / 3 = 1.633.

Also, this average memory access time in CPI is only applicable to 25% of the instructions so AMAT * 0.25 = 1.633 * 0.25 = 0.408333 CPI.

Then in terms of IPC = 1.0 / CPI = 1.0 / 0.408333 = 2.449 IPC.

Thus the achievable IPC of this system with abundant multithreading is 2.449.

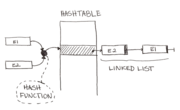
2. Inverted page tables reduce page table space overhead via hashing. However, how are hashing collisions handled? Explain any policy the hardware/operating system may have to use.

One method to handle hashing collisions is to use chaining. To implement chaining, linked lists are often used. When storing a new value in the hash table at an index that's already occupied (i.e., there is a collision), the value can be appended to the end of the linked list. When either of the values is needed later, the linked list will then be searched to find the correct value to be returned.

If the hashing algorithm is good and the hash table has a decent size, the number of collisions should be minimal and an amortized store / access time of O(1) can be expected. In the worst case, however, everything will hash to the same index within the hash table and gets stored within a linked list. In this scenario, access times are that of a linear search, O(n), as the entire linked list may have to be explored.

In summary, chaining is one policy a hash table can use to handle hashing collisions.

III. Multicore

1. Assuming non-atomic writes, add statements to the following code to show sequential consistency (SC) violation. You may add statements to one or both threads, and either before or after the statements shown below.

Assume that before the following code segment runs X=Y=0.

Thread 1: write X = 10;
Thread 2: write Y = 20;

Show your new code and explain how SC may be violated.

The added statements are shown below in bold.

Thread 1 Code: write X = 10; print Y;

Thread 2 Code: write Y = 20; print X;

Sequential consistency may be violated when both Thread 1 prints "Y = 0" and Thread 2 prints "X = 0." In a sequentially consistent system, either Thread 1 should print "Y = 20" and/or Thread 2 should print "X = 10."

2. Assume the following multithreaded code where mypid is each thread's process id. The thread runs on n cores with coherent private caches.

(a) Explain why this code is likely to perform poorly.

(b) Describe how to address this problem and show your pseudocode.

(a) I think the code is likely to perform poorly due to overhead imposed by keeping the data structure A coherent across the many different (n cores) private caches. Given the A += A... operator, there is a read for each write. Then to keep everything coherent, before each read, the caches needs to make sure all pending writes occur, before any read, across every core. This is the root of the overhead.

(b) If I understand the code segment correctly: One idea could be to break A into localized segments - one for each core or thread to work on - in a structure separate from A. This way, Core / Thread i could perform its own work while minimizing impact to the work of other Cores / Threads. This method is not without its own overhead, however, as there would have to be a merge step after each Thread's work is done to combine all data back into the global data structure, A.

IV. Fundamentals

A high-performance architecture uses ultra-wide simultaneous multi-threaded (SMT) processors (e.g., 128-way SMT processors) to target "embarrassingly" parallel, highly regular and loop-based codes with heavy branching (e.g., highly-conditional dense matrix applications). Due to the heavy branching, vector compiler scheduling is not effective. Instead, the compiler generates simple, parallel threads from the loop iterations each of wich runs on an SMT context (e.g., 128 iterations run in parallel). While the branching disallows lock-step execution across the threads, the iterations are naturally load-balanced and access mostly sequentially-contiguous data (e.g., thread i accesses ith array elements). A key challenge is designing memory system to support such processors which employ a cache hierarchy (memory system includes cache and main memory). Assume the code has enough reuse to justify a conventional cache hierarchy.

1. Which memory-system parameters poses a key challenge for data access? Which parameters are much less relevant?

The most important memory system parameters for data access would be memory bandwidth and memory latency. Other important parameters may be cache size(s) and memory block size. Less relevant parameters may be those such as associativity and replacement policy.

2. Based on the code characteristics listed above, what would be your strategy to address the above challenge? Describe your strategy for both caches and main memory.

If I understood the problem correctly, the issue with the assumed conventional cache hierarchy being used, for each of the 128 processors, is cache coherency / consistency. If such policies are enforced with a snooping protocol, the overhead could be reduced using a directory control method. Another, more drastic change, would be to use a Distributed Shared Memory (DSM) model (vs the conventional SMP model). The DSM model improves upon the two pain points mentioned above: it increases memory bandwidth and decreases memory latency.

3. What difficulty does the lack of lock-stepping cause your strategy? How would you tackle the difficulty?

A lack of lock step implies that each processor is doing potentially different types of instructions. For example P1 could be producing a value, P2 could be writing a value, P3 could be reading a value, etc. Without lock step then, our system may enter a non-optimal / unbalanced state. More specifically, under these conditions cache coherency becomes an issue as each Processor's cache is most likely not consistent, thus causing potential overhead in terms of increased memory latency. As mentioned above, these effects could be potentially lessened by using a Distributed Shared Memory (DSM) hierarchy in lieu of the traditional (SMP) memory hierarchy.