ECE-QE-CE-4-2015 - Rhea

ECE Ph.D. Qualifying Exam
Computer Engineering, Question 04 (CE-4): Architecture
August 2015

I. Processor

In modern out-of-order processors pipelines, there are many "pipeline loops" due to data/information generated in later pipeline stages and used in earlier stages (e.g., register bypass, branch resolution, and rename table update). Modern pipelines have many such loops each of which is relevant only to a subset of instructions.

Assume single-issue pipeline for the following questions.

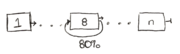
1. What is the increase in the cycles per instruction (CPI), if 80% of instructions incur a loop from the 8th stage to the 8th stage? Also, give a real example of such a loop.

SOLUTION #1

Assuming each stage can be completed in one cycle: If 80% of instructions incur a one cycle/stage loop-back, this implies that stage would have to be performed again. Thus, a one cycle penalty for 80% instructions would result in a 1 * 0.8 = 0.8 CPI increase.

An example of such a loop may be found either in incrementers (i++) or decrementers (i--).

SOLUTION #2

0.8 CPI increase. (1 x 0.8). An example of this loop can be found in ALU: a = a + 1.

2. For a loop from the 15th stage back to the 1st stage, the pipeline employs prediction with accuracy 90% (you should figure out how prediction lessens the loops' impact on the CPI). What is the increase in the CPI if the loop is relevant to 20% of all instructions?

SOLUTION #1

• For 20% of instructions, there is a pipeline loop from the 15th to the 1st stage.
• For 90% of such instructions, the pipeline can predict this behavior.

So 18% (0.2 * 0.9) of instructions loop from the 15th stage to the 1st stage in a predicted manner. This means that 2% (0.2 * 0.1) of instructions loop from the 15th stage to the 1st stage without prediction and must pay a penalty. This penalty is where the increase in CPI will originate. When a misprediction occurs, the penalty here is 15 stages/cycles which 2% of instructions must pay.

Therefore, 0.02 * 15 cycles/stages = 0.3 increase in CPI. If the correctly predicted loop back from the 15th to the 1st stage does not have to pay the penalty (I assume this here due to the nature of the correct prediction), then 0.3 is the total increase to the CPI.

SOLUTION #2

0.3 CPI increase. (15 x 0.2 x 0.1).

3. For a loop from the 15th stage back to the 1st stage and another from the 10th stage back to the 5th stage, if 1% of instructions are affected by the former loop and 3% (including the previous 1%) are affected by the latter loop, what is the increase in CPI?

SOLUTION #1

From the question we know that a loop back from the 15th to the 1st stage equates to a 15 cycle/stage penalty. A loop then from the 10th stage back to the 5th stage is a cycle/stage penalty (as stages 5, 6, 7, 8, 9, and 10 all have to be visited again).

Then we know that 1% of instructions pay the 15 stage/cycle penalty and 3% of instructions pay the 6 stage/cycle penalty.

The problem states that this 3% "includes the previous 1%." Given this, to calculate the affect of this loop separately, I assume the 3% is instead 2% (3%-1%).

Then:

• 1% pay the 15 stage penalty: 0.01 * 15 = 0.15
• 2% pay the 6 stage penalty: 0.02 * 6 = 0.12

Therefore, the total increase to the system CPI imposed by these two loop-backs is 0.27 CPI.

SOLUTION #2

0.33 CPI increase. (15 x 0.01 + 6 x 0.03) = 0.15 + 0.18 = 0.33.

Discussion:

• Part 1 and Part 2 have the same solutions.
• The solutions for Part 3 differ, and the difference is in how the "including the previous 1%" is interpreted and used within the calculations. Solution #1's calculation of 2% (using 3%-1%) may be too simplistic, yet Solution #2's solution may count certain loops more than once.

Related Problem(s):

1. 99% of instructions incur a loop from the 12th to the 12th stage, and it can be predicted with 75% accuracy. What is the increase in CPI in this instance?
2. A loop from the 11th to 7th stage affects 2% of instructions and can be predicted with 50% accuracy. A loop from the 10th to 8th stage affects 5% of instructions (including the previous 2%) and it can be predicted with 95% accuracy. What is the increase in CPI in this instance?
3. For the above problems, what would change if a single-issue pipeline was no longer assumed?

II. Memory systems

1. Assume 25% of all instructions are loads and stores, L1 miss rate is 20%, L2 miss rate is 20% (out of L1 misses), and L1, L2, main memory latencies are 3, 32, and 300 cycles, respectively, and their bandwidths are, respectively, 1 access (hit or miss) every 1, 8, and 30 cycles. What is the achievable IPC (instructions per cycle), if we assume abundant parallelism due to simultaneous multithreading?

SOLUTION #1

The question says we can assume abundant parallelism due to simultaneous multithreading. For my solution, I take this to mean that when a memory component (L1, L2, or main memory) misses, other instructions can still use this memory unit (up until the memory unit's bandwidth cap has been reached).

• So since L1's latency is 3 cycles and it can do one access every 1 cycle, this means that it can handle 3 (3 / 1 ) overlapping operations at one time.
• L2's latency is 32 cycles and it can do one access every 8 cycles. This means that it can handle 4 (32 / 8 ) overlapping operations at one time.
• Main memory's (MM's) latency is 300 cycles and it can do one access every 30 cycles. This means that it can handle 10 (300 / 30) overlapping operations at one time.

We know average memory access time (AMAT) can be calculated: hit time + (miss rate * miss penalty). We can use this to help calculate the achievable IPC such as,

AMAT (in CPI) = (L1_hitTime + L1_missRate * L1_missPenalty) / L1_nOverlap,

where

L1_missPenalty = (L2_hitTime + L2_missRate * L2_missPenalty) / L2_nOverlap

and

L2_missPenalty = (MM_{hitTime) / MMnOverlap.}

Using the problem's parameters:

L2_missPenalty = 300 / 10 = 30.

L1_missPenalty = (32 + 0.2 * 30) / 4 = 9.5.

AMAT = (3 + 0.2 * 9.5) / 3 = 1.633.

Also, this average memory access time in CPI is only applicable to 25% of the instructions so AMAT * 0.25 = 1.633 * 0.25 = 0.408333 CPI.

Then in terms of IPC = 1.0 / CPI = 1.0 / 0.408333 = 2.449 IPC.

Thus the achievable IPC of this system with abundant multithreading is 2.449.

SOLUTION #2

Since the question wants us to assume abundant parallelism, then I think the pipeline doesn't have to stall just because a miss occurs, but it does have to stall if a miss can't be serviced. (Think structural hazard instead of data hazard.) Thus, the only thing stalling the pipeline in this case is the bandwidth.

For L1, a latency of 3 cycles with a bandwidth of 1 access per cycle means that 3 accesses can be serviced simultaneously, which overlaps the penalty. Therefore, since we know there is 1 L1 access every 4 instructions, then the max IPC (just considering L1) is 4.0 IPC (i.e. every cycle, 4 instructions complete, one of which is a load/store).

For L2, a latency of 32 cycles with a bandwidth of 1 access per 8 cycles means that 4 accesses can be serviced simultaneously, which overlaps the penalty. Therefore, since we know there is 1 L2 access every 20 instructions, then the max IPC (just considering L2) is 2.5 IPC (i.e. every 32 cycles, 80 instructions complete, 4 of which are L2 accesses).

For Main Memory (MM), a latency of 300 cycles with a bandwidth of 1 access per 30 cycles means that 10 accesses can be serviced simultaneously, which overlaps the penalty. Therefore, since we know that there is 1 MM access every 100 instructions, then the max IPC (just considering MM) is 3.33 IPC (i.e. every 300 cycles, 1000 instructions complete, 10 of which are MM accesses).

Since the question says to assume abundant parallelism due to simultaneous multithreading, we can assume that these are all independent bottlenecks, so L2 is the limiting factor, giving us a max IPC of 2.5.

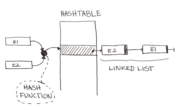
2. Inverted page tables reduce page table space overhead via hashing. However, how are hashing collisions handled? Explain any policy the hardware/operating system may have to use.

SOLUTION #1

One method to handle hashing collisions is to use chaining. To implement chaining, linked lists are often used. When storing a new value in the hash table at an index that's already occupied (i.e., there is a collision), the value can be appended to the end of the linked list. When either of the values is needed later, the linked list will then be searched to find the correct value to be returned.

If the hashing algorithm is good and the hash table has a decent size, the number of collisions should be minimal and an amortized store / access time of O(1) can be expected. In the worst case, however, everything will hash to the same index within the hash table and gets stored within a linked list. In this scenario, access times are that of a linear search, O(n), as the entire linked list may have to be explored.

In summary, chaining is one policy a hash table can use to handle hashing collisions.

SOLUTION #2

Chaining can be used to handle hashing collisions.

Discussion:

• In each solution to Part 1, the overlap (due to parallelism) is calculated the same. The solutions differ, however, and it appears the difference lies in if the components are treated separately or combined. Solution #1 treats the system as a whole: MM affects L2 affects L1. Solution #2 treats each component of the system as an individual piece and says the bottleneck (of the system as a whole) lies within the component with the lowest IPC. Solution #1 here may be the correct approach to this problem as it treats the system as a whole: the work L2 has to do depends on L1's parameters, the work MM has to do depends on L2's (and thus L1's parameters), etc. Since the IPC is for the system as a whole, this approach may make the most sense.
• The solutions to Part 2 are the same: both solutions suggest the common method of chaining to resolve hashing collisions.

Related Problem(s):

1. Assume 30% of instructions are load and stores. The L1 miss rate is 20%, the L2 miss rate is 40% (of the L1 misses), and the L1, L2, and main memory (MM) latencies are respectively 10, 100, 1000 cycles. The bandwidths of each component are respectively 1 access (hit or miss) every 1, 10, and 100 cycles. What is the achievable IPC if we do not assume abundant parallelism due to simultaneous multithreading?
2. (Since chaining is a commonly known solution to handling hashing collisions) What are the drawbacks (hint: think worst case performance) to using chaining with a linked list to handle hashing collisions? Consider what might happen if the hash table is very small or if the hash function is poor. What methods other than chaining with a linked list or in general may be used to resolve hashing collisions?

III. Multicore

1. Assuming non-atomic writes, add statements to the following code to show sequential consistency (SC) violation. You may add statements to one or both threads, and either before or after the statements shown below.

Assume that before the following code segment runs X=Y=0.

Thread 1: write X = 10;
Thread 2: write Y = 20;

Show your new code and explain how SC may be violated.

SOLUTION #1

The added statements are shown below in bold.

Thread 1 Code: write X = 10; print Y;

Thread 2 Code: write Y = 20; print X;

Sequential consistency may be violated when both Thread 1 prints "Y = 0" and Thread 2 prints "X = 0." In a sequentially consistent system, either Thread 1 should print "Y = 20" and/or Thread 2 should print "X = 10."

SOLUTION #2

T1: write Y = 10; write X = 10;

T2: write X = 20; write Y = 20;

Sequential consistency is valid for (x = 10, y = 10) when T2 before T1; (x = 20, y = 20) when T2 after T1; (x = 10, y = 20) when T1 inside T2 or T2 inside T1.

Sequential consistency is invalid for (x = 20, y = 10) which would imply T1's "later" write to X happened "before" T2's write to X and T1's write to Y happened "later" than T2's write to Y.

2. Assume the following multithreaded code where mypid is each thread's process id. The thread runs on n cores with coherent private caches.

(a) Explain why this code is likely to perform poorly.

(b) Describe how to address this problem and show your pseudocode.

SOLUTION #1

(a) I think the code is likely to perform poorly due to overhead imposed by keeping the data structure A coherent across the many different (n cores) private caches. Given the A += A... operator, there is a read for each write. Then to keep everything coherent, before each read, the caches needs to make sure all pending writes occur, before any read, across every core. This is the root of the overhead.

(b) If I understand the code segment correctly: One idea could be to break A into localized segments - one for each core or thread to work on - in a structure separate from A. This way, Core / Thread i could perform its own work while minimizing impact to the work of other Cores / Threads. This method is not without its own overhead, however, as there would have to be a merge step after each Thread's work is done to combine all data back into the global data structure, A.

SOLUTION #2

(a) The array elements could reside in the same block, invalidating all other cache entries and causing thrashing.

(b) Can address the problem by modifying values using an array of pointers instead of modifying the values within A directly. This ensures the pointers are all in the same block (for each process) and not spread all around (like the values of A may be).

Discussion:

• For Part 1 of Solution #2, it is questionable if this scenario - the one in which consistency is violated - can ever exist. The scenarios for which sequential consistency is valid seem to cover the entire realm of possibilities: T1/T1/T2/T2, T2/T2/T1/T1, T1/T2/T1/T2, and T2/T1/T2/T1. The case of (x = 20, y = 10) seems to only occur after T2/T1 or T1/T2 (i.e., in the middle of execution).
• For Part 2 (a), both solutions argued the same point. Each solution approached Part 2 (b) differently, however. Solution #1's approach may work, however the overhead of the merge step may be just as much as the original thrashing, thus not solving the issue. Solution #2 may work, however, it depends on where the pointers are actually kept in memory. Depending on this, the same situation may arise using pointers to access the memory in lieu of directly accessing it.

Related Problem(s):

1. Let X = Y = -1, Thread 1: X = 21; Print Y;, Thread 2: Y = 12; Print X;. Is sequential consistency kept if Thread 1 and Thread 2 both print -1? What are all the consistent combinations of printed outputs?
2. How does cache coherency impact the use of synchronization locks? Might one lock type be better for non-coherent caches versus coherent caches?

IV. Fundamentals

A high-performance architecture uses ultra-wide simultaneous multi-threaded (SMT) processors (e.g., 128-way SMT processors) to target "embarrassingly" parallel, highly regular and loop-based codes with heavy branching (e.g., highly-conditional dense matrix applications). Due to the heavy branching, vector compiler scheduling is not effective. Instead, the compiler generates simple, parallel threads from the loop iterations each of which runs on an SMT context (e.g., 128 iterations run in parallel). While the branching disallows lock-step execution across the threads, the iterations are naturally load-balanced and access mostly sequentially-contiguous data (e.g., thread i accesses ith array elements). A key challenge is designing memory system to support such processors which employ a cache hierarchy (memory system includes cache and main memory). Assume the code has enough reuse to justify a conventional cache hierarchy.

1. Which memory-system parameters poses a key challenge for data access? Which parameters are much less relevant?

SOLUTION #1

The most important memory system parameters for data access would be memory bandwidth and memory latency. Other important parameters may be cache size(s) and memory block size. Less relevant parameters may be those such as associativity and replacement policy.

SOLUTION #2

Block size would be important while instruction cache size may be less important.

2. Based on the code characteristics listed above, what would be your strategy to address the above challenge? Describe your strategy for both caches and main memory.

SOLUTION #1

If I understood the problem correctly, the issue with the assumed conventional cache hierarchy being used, for each of the 128 processors, is cache coherency / consistency. If such policies are enforced with a snooping protocol, the overhead could be reduced using a directory control method. Another, more drastic change, would be to use a Distributed Shared Memory (DSM) model (vs the conventional SMP model). The DSM model improves upon the two pain points mentioned above: it increases memory bandwidth and decreases memory latency.

SOLUTION #2

Using word-sized cache blocks would help pull in extra data on each cache miss.

3. What difficulty does the lack of lock-stepping cause your strategy? How would you tackle the difficulty?

SOLUTION #1

A lack of lock step implies that each processor is doing potentially different types of instructions. For example P1 could be producing a value, P2 could be writing a value, P3 could be reading a value, etc. Without lock step then, our system may enter a non-optimal / unbalanced state. More specifically, under these conditions cache coherency becomes an issue as each Processor's cache is most likely not consistent, thus causing potential overhead in terms of increased memory latency. As mentioned above, these effects could be potentially lessened by using a Distributed Shared Memory (DSM) hierarchy in lieu of the traditional (SMP) memory hierarchy.

SOLUTION #2

As threads are out-of-sync, the working set for the cache increases. This can be addressed potentially with a shared (between threads) instruction cache and a victim buffer.

Discussion:

• For Part 1, both solutions thought that block size would be one of the important memory parameters.
• For Part 2, the approach by Solution #2 is a little unclear. Using the solution along with the problem's description of thread i accesses ith array elements then perhaps this could be beneficial. If on a miss it can be estimated that the following elements, etc. will also miss, a larger block of memory being loaded in could help lessen future misses. Solution #1 assumed the memory scheme (to DSM) was within the bounds of the problem description.
• For Part 3, each solution attributes the lack of lock-step to differing problems. Solution #1's approach aims to solve the cache coherency problem caused by a lack of lock step. Solution #2's approach aims to solve the increased working set for the caches. Solution #2's use of a victim buffer is a little unclear, however, it may make sense in the context of the instruction cache. If Processor 1 is performing Instruction A, Processor 2 may perform Instr. A some time afterward (due to the lack of lock-step) and may be able to load the instruction from the victim buffer. It is unclear how much impact a victim buffer on the (shared) instruction cache would improve overall performance, however, since there would be potentially 128 processors sharing the same (out of step) instruction cache.

Related Problem(s):

1. In a system as described above, how would the considerations change if the iterations were instead not naturally load-balanced and did not access mostly sequentially-contiguous data?
2. Why does heavy branching render vector compiler scheduling not effective (re: the above problem, IV. Fundamentals)?
3. Why does the branching disallow lock-step execution across the threads (re: the above problem, IV. Fundamentals)?