Difference between revisions of "CBR logistic regression" - Rhea

Revision as of 20:52, 13 May 2014

Logistic regression

A slecture by ECE student Borui Chen

Partly based on the ECE662 Spring 2014 lecture material of Prof. Mireille Boutin.

Introduction

In the field of machine learning, one big topic is classification problem. A linear classifier is an algorithm that make the classification decision on a new test data point base on a linear combination of the features.

There are two classes of linear classifier: Generative model and Discriminative model:

The generative model measures the joint distribution of the data and class.
- Examples are Naive Bayes Classifier, Linear Discriminant Analysis.

The discriminivative model makes no assumption on the joint distribution of the data. Instead, it takes the data as given and tries to maximize the conditional density (Prob(class|data)) directly.
- Examples are Logistic Regression, Perceptron and Support Vector Machine.

Intuition and derivation of Logistic Regression

Consider a simple classification problem. The goal is to tell whether a person is male or female base on one feature: hair length. The data is given as $$ (x_i,y_i) $$ where i is the index number of the training set, and $$ x_i $$ is hair length in inches and $$ y_i=1 $$ indicates the person is male and 0 if female. Assume women has longer hair length the distribution of training data will look like this:

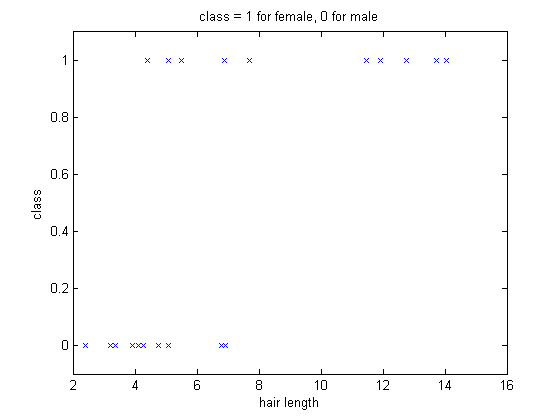
Clearly if a person's hair length is comparably long, being a female is more likely. If there is another person with hair length 10, we could say it's more likely to be a female. However, we don't have a description about how long is long enough to say a person is female. So we introduce the probability.

The intuition of logistic regression, in this example, is to assign a continuous probability to every possible value of hair length so that for longer hair length the probability of being a female is close to 1 and for shorter hair length the probability of being a female is close to 0. It is done by taking the linear combination of the feature and a constant and feeding it into a logistic function:

\begin{align} a_i &= \beta_0+\beta_1 x_i\\ &=\beta^T x_i \end{align}

L(a) = \frac{1}{1+e^{(-a)}}

Then the logistic function of $$ x_i $$ would be:

L(x_i) = Pr(Y_i=1|x_i) = Pr(female|x_i)= \frac{1}{1+e^{(-\beta^T x_i)}}

After some fitting optimization algorithm, the curve looks like the following:

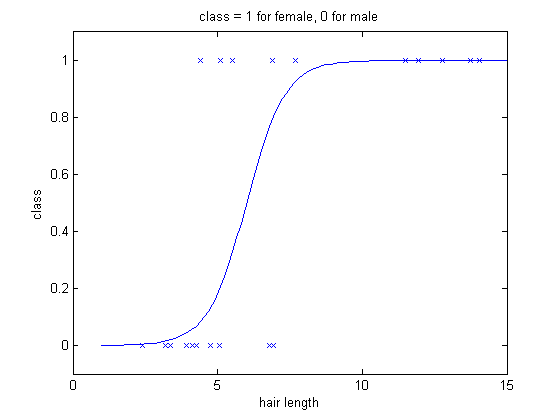
Having this curve, we could develop an decision rule:

\text{This person is } \begin{cases} female, & \text{if }L(x_i)\ge 0.5\\ male, & \text{if }L(x_i) < 0.5 \end{cases}

More generally, the feature can be more than one dimension

$ x = (1,x_1,x_2,...,x_n)^T $

\beta = (\beta_0,\beta_1,\beta_2,...,\beta_n)^T

Note:

the decision boundary is linear:

\beta^T x_i = 0

For 1-D it's a point, 2-D it's a line and etc.

$\beta^T x_i$ is the log of the odd ratio:

\beta^T x_i = log\frac{Pr(female)}{Pr(male)}=log\frac{Pr(female)}{1-Pr(female)}

Having this setup, the goal is to find a $\beta$ to let the curve fit the data optimally. It comes about Maximum Likelihood Estimation and Newton's method.

Maximum Likelihood Estimation

For the logistic regression, we need to figure out a best fit of the curve to the training data. To do this, we choose $\beta$ such that the likelihood of the joint distribution of the training data

$ Pr(Y_1=y_1,...,Y_n=y_n|x_1...x_n) $

is maximized.

From the likelihood function:

\begin{align} Pr(y|x) \triangleq Pr(Y_1=y_1,...,Y_n=y_n|x_1...x_n) &= \prod_{i=1}^n Pr(Y_i=y_i|x_i,\beta)\\ &= \prod_{i=1}^n Pr(Y_i=1|x_i,\beta)^{y_i} Pr(Y_i=0|x_i,\beta)^{1-y_i} \end{align}

For simple notation, let

\alpha = Pr(y_i=1|x_i,\beta)=\frac{1}{1+e^{-\beta^T x_i}}

Take the log of the likelihood function:

\begin{align} \log Pr(y|x) &= \sum_{i=1}^n y_i \log Pr(Y_i=1|x_i,\beta) + (1-y_i)\log Pr(Y_i=0|x_i,\beta)\\ &\triangleq \sum_{i=1}^n y_i \log \alpha + (1-y_i)\log (1-\alpha)\\ \end{align}

where

\begin{align} \alpha_i &= Pr(Y_i=1|x_i,\beta)=\frac{1}{1+e^{(-\beta^T x_i)}}\\ 1-\alpha_i &= Pr(Y_i=0|x_i,\beta)=\frac{1}{1+e^{(\beta^T x_i)}} \end{align}

and

\frac{\partial}{\partial\beta_j}\log \alpha_i = \frac{x_{ij}e^{-\beta^T x}}{1+e^{-\beta^T x}}=x_{ij}(1-\alpha)

\frac{\partial}{\partial\beta_j}\log (1-\alpha_i) = -x_{ij}+x_{ij}(1-\alpha)=-\alpha x_{ij}

Taking the derivative of the log likelihood with respect to $\beta$ :

\begin{align} \frac{\partial}{\partial\beta_j}\log Pr(y|x)&=\sum_{i=1}^n y_ix_{ij}(1-\alpha_i)-(1-y_i)x_{ij}\alpha_i\\ &= \sum_{i=1}^n y_i x_{ij}(1-\alpha_i) -(1-y_i)\alpha_i x_{ij} &= \sum_{i=1}^n (y_i - \alpha_i)x_{ij} \end{align}

If we set the above equation to zero, there is no close form solution, so we are going to use numerical optimization method to maximized the likelihood, namely, Newton's method.

Numerical optimization - Newton's method

To apply the Newton's method, we need a gradient function of log likelihood with respect to $\beta$ , together with a Hessian matrix. from the last part, we've already computed the derivative for each $\beta_i$ , now we need to write it in matrix form.

@@ Line 120: / Line 120: @@
 </math></center>
-Taking the derivative with respect to <math>\beta</math>:
+and
+<center><math>
+\frac{\partial}{\partial\beta_j}\log \alpha_i = \frac{x_{ij}e^{-\beta^T x}}{1+e^{-\beta^T x}}=x_{ij}(1-\alpha)
+</math></center>
+<center><math>
+\frac{\partial}{\partial\beta_j}\log (1-\alpha_i) = -x_{ij}+x_{ij}(1-\alpha)=-\alpha x_{ij}
+</math></center>
+Taking the derivative of the log likelihood with respect to <math>\beta</math>:
 <center><math>
 \begin{align}
-\frac{\partial}{\partial\beta_j}\log Pr(y|x)&=\sum_{i=1}^n y_ix_{ij}(1-\alpha_i)-(1-y_i)x_{ij}\alpha_i
+\frac{\partial}{\partial\beta_j}\log Pr(y|x)&=\sum_{i=1}^n y_ix_{ij}(1-\alpha_i)-(1-y_i)x_{ij}\alpha_i\\
+&= \sum_{i=1}^n y_i x_{ij}(1-\alpha_i) -(1-y_i)\alpha_i x_{ij}
+&= \sum_{i=1}^n (y_i - \alpha_i)x_{ij}
 \end{align}
 </math></center>
+If we set the above equation to zero, there is no close form solution, so we are going to use numerical optimization method to maximized the likelihood, namely, Newton's method.
 ----
-== Numerical optimization ==
+== Numerical optimization - Newton's method ==
+To apply the Newton's method, we need a gradient function of log likelihood with respect to <math>\beta</math>, together with a Hessian matrix. from the last part, we've already computed the derivative for each <math>\beta_i</math>, now we need to write it in matrix form.