| Line 53: | Line 53: | ||
<center> | <center> | ||
| − | [[Image:pw_figure3.png| | + | [[Image:pw_figure3.png|900px]] |
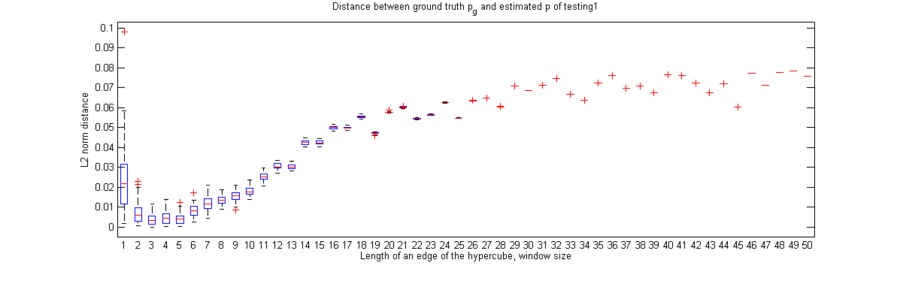
Figure 3. L2 norm distance between ground truth $p$ and estimated <math>p_n</math>. | Figure 3. L2 norm distance between ground truth $p$ and estimated <math>p_n</math>. | ||
Revision as of 07:40, 30 April 2014
Parzen window method and classification
A slecture by ECE student Chiho Choi
Partly based on the ECE662 Spring 2014 lecture material of Prof. Mireille Boutin.
in progress....
Unlike parametric density estimation methods, non-parametric approaches locally estimate density function by a small number of neighboring samples [4] and therefore show less accurate estimation results. In spite of their accuracy, however, the performance of classifiers designed using these estimates is very satisfactory.
The basic idea for estimating unknown density function is based on the fact that the probability $ P $ that a vector x belongs to a region $ R $ [1]:
It can be rewritten as
if we assume a small local region $ R $, a large number of samples $ n $, and $ k $ of $ n $ falling in $ R $.\\ Suppose that the region $ R $ is a $ d $-dimensional hypercube around $ \textbf{x}_i \in \mathbb{R}^n $ in the rest of this slecture, and let the volume $ V_n $:
where $ h_n $ is the length of an edge. Then the window function for this hypercube can be defined by
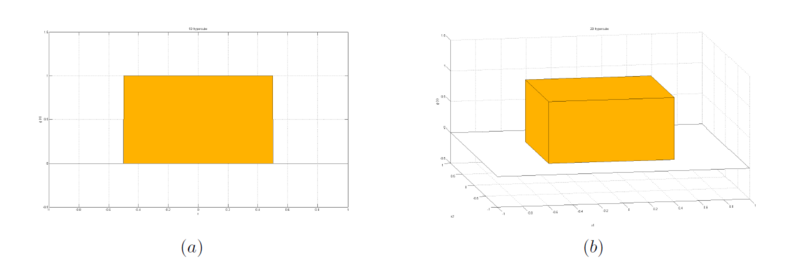
Figure 1. Given window function. (a) where $ d $ = 1, (b) where $ d $ = 2.
We simply shift this window function for $ \textbf{x}_i $ to determine if $ \textbf{x}_i $ belongs to the volume $ V_n $, $ \varphi(\frac{\textbf{x} - \textbf{x}_i}{h_n}) $, and can compute the number of samples $ k_n $ falling in this volume using it:
In Parzen window method, therefore, the estimate for density $ p_n(\textbf{x}) $ is
In order to check how window length effects on $ p_n(\textbf{x}) $, we define $ \delta_n(\textbf{x} - \textbf{x}_i) $ by $ \frac{1}{V_n} \varphi(\frac{\textbf{x} - \textbf{x}_i}{h_n}) $ as an approximation of a unit impulse centered at $ \textbf{x}_i $ [2] and write $ p_n(\textbf{x}) $ [1] by:
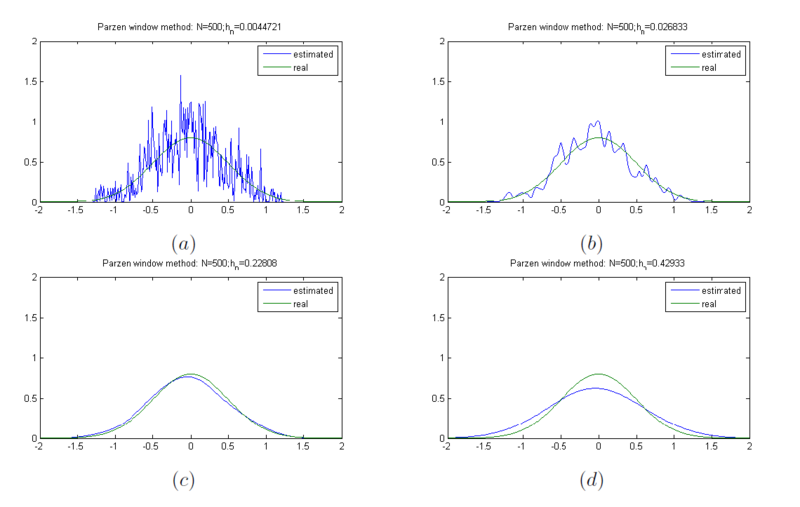
From this observation, we can infer the relationship between $ h_n $ and $ p_n(\textbf{x}) $. If $ h_n $ is very large, the amplitude of $ \delta_n $ is small because $ V_n = h_n^d $. Thus, $ p_n(\textbf{x}) $ becomes a very smooth estimate for $ p(\textbf{x}) $. In contrast, if $ h_n $ is very small, the amplitude of $ \delta_n $ is large. As a result, $ p_n(\textbf{x}) $ is a noisy estimate for $ p(\textbf{x}) $. Therefore, when we have a limited number of samples, to find out an optimal value of $ h_n $ is very important to estimate $ p(\textbf{x}) $. Let us assume that we have an unlimited number of samples. Then, $ V_n $ goes to zero as $n$ increases, and hence $ p_n(\textbf{x}) $ converges to $ p(\textbf{x}) $ [1] no matter what $ h_n $ is.
Figure 2. Density estimate using Parzen window where N = 500. (a) $ h_n $ = 0.0044, (b) $ h_n $ = 0.0268, (c) $ h_n $ = 0.2280, and (d) $ h_n $ = 0.4293.
Figure 3. L2 norm distance between ground truth $p$ and estimated $ p_n $.
Post your slecture material here. Guidelines:
- If you are making a text slecture
- Type text using wikitext markup languages
- Type all equations using latex code between <math> </math> tags.
- You may include links to other Project Rhea pages.
$ \rightarrow $
Questions and comments
If you have any questions, comments, etc. please post them on this page.