| Line 34: | Line 34: | ||
{equation of estimated density at x here} | {equation of estimated density at x here} | ||
| − | We approximate the density p(x) by, | + | We approximate the density p(x) by, <br/> |
{equation here } <br/> | {equation here } <br/> | ||
| + | Most of the time this estimate is, {equation here} <br/> | ||
| + | == How to classify data using k-NN Density Estimate == | ||
| + | Having seen how the density at a given point x is estimated based on the value of k and the given observations x<sub>1</sub>,x<sub>2</sub>,x<sub>3</sub>,...,x<sub>n</sub>, let's discuss about using the k-NN density estimate for classification. </br> | ||
| − | + | <b>Method 1:<b> <br/> | |
| − | + | ||
| − | + | Let x<sub>0</sub> from R<sup>n</sup> be a point to classify. | |
| − | + | ||
| − | + | Given are samples x<sub>i1</sub>,x<sub>x2</sub>,..,x<sub>xn</sub> for i classes. <br/> | |
| + | |||
| + | We now pick a k<sub>i</sub> for each class and a window function, and we try to approximate the density at x<sub>0</sub> for each class and then pick the class with the largest density based on, <br/> | ||
| + | |||
| + | {equation here} | ||
| + | |||
| + | If the priors of the classes are unknown, we use ROC curves to estimate the priors, based on, | ||
| + | |||
| + | {equation here} | ||
| + | |||
| + | <b>Method 2:<b> </br> | ||
| + | |||
| + | Given are samples x<sub>i1</sub>,x<sub>x2</sub>,..,x<sub>xn</sub> from a Gaussian Mixture. We choose a single value of k and and one window function, <br/> | ||
| + | |||
| + | We then approximate p(x, w<sub>i</sub>) by, <br/> | ||
| + | {equation here}</br> | ||
| + | |||
| + | where V<sub>i</sub> is the volume of the smallest window that contains k samples and k<sub>i<sub> is the number of samples among these k that belongs to class i. <br/> | ||
| Line 49: | Line 69: | ||
---- | ---- | ||
---- | ---- | ||
| + | |||
| + | Post your slecture material here. Guidelines: | ||
| + | *If you are making a text slecture | ||
| + | **Type text using wikitext markup languages | ||
| + | **Type all equations using latex code between <nowiki> <math> </math> </nowiki> tags. | ||
| + | **You may include links to other [https://www.projectrhea.org/learning/about_Rhea.php Project Rhea] pages. | ||
==[[slecture_title_of_slecture_review|Questions and comments]]== | ==[[slecture_title_of_slecture_review|Questions and comments]]== | ||
Revision as of 18:47, 24 April 2014
K-Nearest Neighbors Density Estimation
A slecture by CIT student Raj Praveen Selvaraj
Partly based on the ECE662 Spring 2014 lecture material of Prof. Mireille Boutin.
Contents
Introduction
This slecture discusses about the K-Nearest Neighbors(k-NN) approach to estimate the density of a given distribution. The approach of K-Nearest Neighbors is very popular in signal and image processing for clustering and classification of patterns. It is an non-parametric density estimation technique which lets the region volume be a function of the training data. We will discuss the basic principle behind the k-NN approach to estimate density at a point X and then move on to building a classifier using the k-NN Density estimate.
Basic Principle
The general formulation for density estimation states that, for N Observations x1,x2,x3,...,xn the density at a point x can be approximated by the following function,
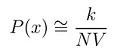
where V is the volume of some neighborhood(say A) around x and k denotes the number of observations that are contained within the neighborhood.
The basic idea of k-NN is to extend the neighborhood, until the k nearest values are included. If we consider the neighborhood around x as a sphere, for the given N Observations, we pick an integer,
{an equation goes here}
If xl is the kth closest sample point to x, then hk = ||xl - x||
{equation of estimated density at x here}
We approximate the density p(x) by,
{equation here }
Most of the time this estimate is, {equation here}
How to classify data using k-NN Density Estimate
Having seen how the density at a given point x is estimated based on the value of k and the given observations x1,x2,x3,...,xn, let's discuss about using the k-NN density estimate for classification. </br>
Method 1:<b>
Let x0 from Rn be a point to classify.
Given are samples xi1,xx2,..,xxn for i classes.
We now pick a ki for each class and a window function, and we try to approximate the density at x0 for each class and then pick the class with the largest density based on,
{equation here}
If the priors of the classes are unknown, we use ROC curves to estimate the priors, based on,
{equation here}
<b>Method 2:<b> </br>
Given are samples xi1,xx2,..,xxn from a Gaussian Mixture. We choose a single value of k and and one window function,
We then approximate p(x, wi) by,
{equation here}</br>
where Vi is the volume of the smallest window that contains k samples and ki is the number of samples among these k that belongs to class i.
Post your slecture material here. Guidelines:
- If you are making a text slecture
- Type text using wikitext markup languages
- Type all equations using latex code between <math> </math> tags.
- You may include links to other Project Rhea pages.
Questions and comments
If you have any questions, comments, etc. please post them on this page.

