Revision as of 14:14, 20 October 2015

Homework 7, ECE438, Fall 2015, Prof. Boutin

Hard copy due in class, Wednesday October 14, 2015.

Questions 1

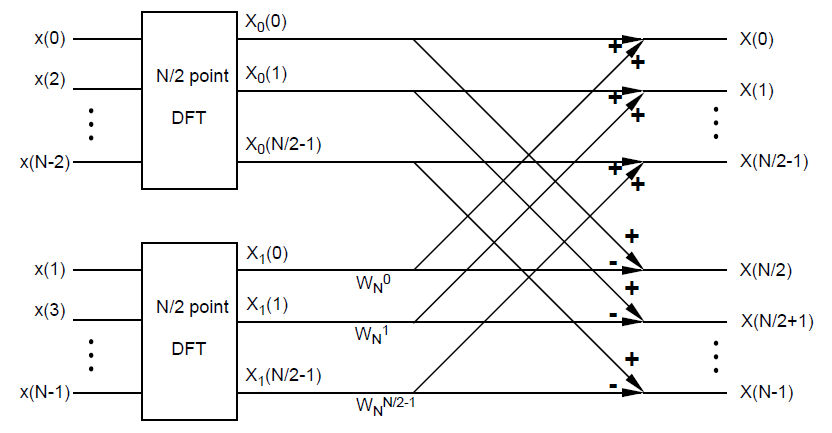
Draw the complete flow diagram for the "decimation by two" FFT algorithm to compute a 122 point DFT. How many complex operations does your algorithm take? How many operations would this DFT computation take if you were using the summation formula (i.e., the definition of the DFT) instead?

Solution

Diagram of "decimation by two" FFT computing N-pt DFT. N=8 in this question.

where $ W_N^k = e^{-j2\pi k/N} $

A direct computation of DFT requires $ N^2 = 14884 $ times of complex multiplications and $ N^2-N = 14762 $ times of complex additions.

Using "decimation by two" FFT algorithm, the total number of multiplications is $ 2\cdot (\frac{N}{2})^2 + \frac{N}{2} = 7503 $ and the total number of additions is $ 2((\frac{N}{2})^2-\frac{N}{2}) + N = 7442 $

Questions 2

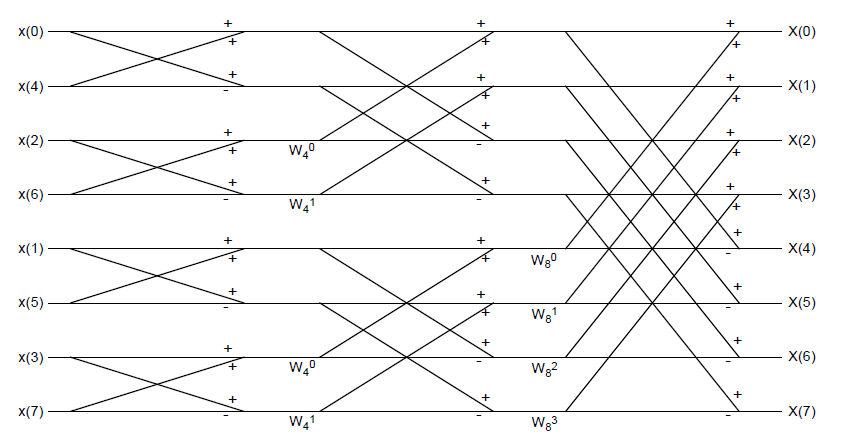
Draw a complete flow diagram for of the "radix-2" FFT algorithm to compute an 8 point DFT. How many complex operations does your algorithm take?

Diagram of "radix-2" FFT computing 8-pt DFT.

where $ W_N^k = e^{-j2\pi k/N} $

Recall the definition of DFT:

$ X[k]=\sum_{n=0}^{N-1} x[n]e^{-j2\pi k/N},\ k=0,...,N-1 $

In this question N=8

If we use summation formula to compute DFT, for each k, we need N times complex multiplications and N-1 times complex additions.

In total, we need N*N=64 times of complex multiplications and N*(N-1)=56 times of complex additions.

In decimation-in-time FFT algorithm, we keep on decimating the number of points by 2 until we get 2 points DFT. At most, we can decimate $ v=log_2 N $ times. As a result, we get v levels of DFT. Except for the first level (2-pt FFT), which only needs N times complex additions, for the rest of levels, we need N/2 times of complex multiplications and N times of complex additions.

In total, we need $ \frac{N}{2}(log_2 N -1)=8 $ times of complex multiplications and $ Nlog_2 N=24 $ times of complex additions.

(Note: when $ N $ is large, $ log_2 N -1 \approx log_2 N $. So the number of multiplications becomes $ \frac{N}{2}log_2 N $.)

Question 3

Use the definition of the DFT (the summation formula) to obtain two different FFT algorithms to compute a 6 point DFT. Draw a flow diagram for each of your algorithms, and compute the total number of complex operations they would require. Compare these two numbers with the number of complex operations this computation would take if you were using the definition of the DFT instead.

Denote N is the points number of the input signal's DFT. In this question N=6.

1) The normal DFT algorithm: If we use summation formula to compute DFT, according to the analysis of Question 1. We need N*N=36 times of complex multiplications and N*(N-1)=30 times of complex additions.

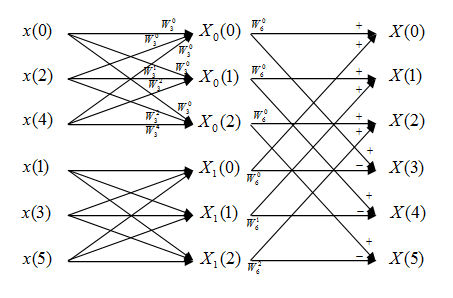
Flow diagram of FFT：

Analytical Expressions:

$ \begin{align} X_6(k)&=\sum_{n=0}^{5} x(n)e^{-\frac{j2\pi kn}{6}} \\ &\text{Change variable n=2m+l, m=0,1,2; l=0,1 } \\ X_6(k)&=\sum_{l=0}^{1}\sum_{m=0}^{2}x(2m+l)e^{-\frac{j2\pi k(2m+l)}{6}} \\ &=\sum_{l=0}^{1}e^{-\frac{j2\pi kl}{6}}\sum_{m=0}^{2}x(2m+l)e^{-\frac{j2\pi km}{3}} \\ &=\sum_{l=0}^{1}W_6^{kl}X_l(k) \text{ ,k=0,1,...,5 } \end{align} $

Note that $ X_l(k) = X_l(k+3),\ k=0,1,2 $

In this FFT algorithm, the computing of DFT is divided into two levels. First, we compute two 3-point DFT, which are DFT of even and odd points.

In this step we need 4 times of complex multiplications (consider when m=0 and k=0,3, there are no multiplies needed) and 6 times of complex additions for each 3-point DFT. Since we have to do this twice, we need 4*2=8 times of complex multiplications and 6*2=12 times of complex additions.

Second, we compute the final DFT by combing the first level result. According to the analysis of Question 1, we need N/2=3 times of complex multiplications and N=6 times of complex additions.

In total, we need 8+3=11 times of complex multiplications and 12+6=18 times of complex additions.

2)

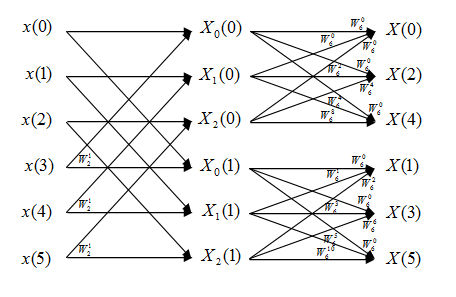
Flow diagram of FFT：

Analytical Expressions:

$ \begin{align} X_6(k)&=\sum_{n=0}^{5} x(n)e^{-\frac{j2\pi kn}{6}} \\ &\text{Change variable n=3m+l, m=0,1; l=0,1,2 } \\ X_6(k)&=\sum_{l=0}^{2}\sum_{m=0}^{1}x(3m+l)e^{-\frac{j2\pi k(3m+l)}{6}} \\ &=\sum_{l=0}^{2}e^{-\frac{j2\pi kl}{6}}\sum_{m=0}^{1}x(3m+l)e^{-\frac{j2\pi km}{2}} \\ &=\sum_{l=0}^{2}W_6^{kl}X_l(k) \text{ ,k=0,1,...,5 } \end{align} $

Note that $ X_l(k) = X_l(k+2) = X_l(k+4),\ k=0,1 $

In this FFT algorithm, the computing of DFT is still divided into two levels. However, we will first compute three 2 points DFT, which are DFT of the first half points and the second half points. According to analysis of Question 1, we need N/2=3 times of complex multiplications and N=6 times of complex additions.

Second, we compute the two 3 points DFT using first level result. we need 4 times of complex multiplications (consider when l=0 and k=0,3 there are no multiplies needed) and 6 times of complex additions for each 3-point DFT. Since we have to do this twice, we need 4*2=8 times of complex multiplications and 6*2=12 times of complex additions.

In total, we need 3+8=11 times of complex multiplications and 6+12=18 times of complex additions.

Note that the output sequences of DFT of 2) is different from 1).

Compare 1) and 2), both methods have the same amount of complex operations.

Discussion

• Write question/comment here.
  • answer will go here

Back to ECE438, Fall 2015, Prof. Boutin