| (29 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
<br> | <br> | ||
<center><font size="4"></font> | <center><font size="4"></font> | ||
| − | <font size="4">'''Neyman-Pearson: How Bayes Decision Rule Controls Error''' <br> </font> <font size="2">A [ | + | <font size="4">'''Neyman-Pearson: How Bayes Decision Rule Controls Error''' <br> </font> <font size="2">A [http://www.projectrhea.org/learning/slectures.php slecture] by Robert Ness </font> |
| − | <font size="2">Partly based on the [[ | + | <font size="2">Partly based on the [[2014_Spring_ECE_662_Boutin_Statistical_Pattern_recognition_slectures|ECE662 Spring 2014 lecture]] material of [[User:Mboutin|Prof. Mireille Boutin]]. </font> |
</center> | </center> | ||
---- | ---- | ||
| Line 10: | Line 10: | ||
'''模式识别''' 的目标是将新观察的特征向量进行分类。为了进行分类的决定,需要通过某种'''判决规则(decision rule)'''。在 '''统计学模式识别''' 一般假设特征向量是个随机变量“X”,又有个概率密度函数或者概率质量函数,并且此函数依赖其分类。假设有两个类型:(<span class="texhtml">ω<sub>0</sub>,ω<sub>1</sub></span>), 以便写公式也不会失去一般性。X的概率密度或质量函数是<span class="texhtml">''f''(''X'' | ω<sub>''i''</sub>)</span> (如下称pdf)。每个类型的'''先验概率'''写成<span class="texhtml">''P''(ω<sub>''i''</sub>)</span>。 | '''模式识别''' 的目标是将新观察的特征向量进行分类。为了进行分类的决定,需要通过某种'''判决规则(decision rule)'''。在 '''统计学模式识别''' 一般假设特征向量是个随机变量“X”,又有个概率密度函数或者概率质量函数,并且此函数依赖其分类。假设有两个类型:(<span class="texhtml">ω<sub>0</sub>,ω<sub>1</sub></span>), 以便写公式也不会失去一般性。X的概率密度或质量函数是<span class="texhtml">''f''(''X'' | ω<sub>''i''</sub>)</span> (如下称pdf)。每个类型的'''先验概率'''写成<span class="texhtml">''P''(ω<sub>''i''</sub>)</span>。 | ||
| − | 两类问题有两种错误:错误选第一类、错误选第二类。下面说明(1)如果用贝叶斯(Bayes)判决规则,等于做似然比检验 (Likelihood Ratio Test),加上(2)Neyman- | + | 两类问题有两种错误:错误选第一类、错误选第二类。下面说明(1)如果用贝叶斯(Bayes)判决规则,等于做似然比检验 (Likelihood Ratio Test),加上(2)Neyman-Pearson引理证明由于在用似然比检验,判决规则能控制一种错误率在一定的数量的同时将另一类的错误率控制在尽可能最少的数量。下面用统计学假设检验(Statistical Hypothesis Test)和标准正常分布(Standard Normal Distribution)作为例子。 |
| − | + | == 似然比检验 == | |
| − | + | ||
似然比统计定义为:<br> | 似然比统计定义为:<br> | ||
<math>\lambda(X)=\frac{f(X|\omega_0)}{f(X|\omega_1)} </math> | <math>\lambda(X)=\frac{f(X|\omega_0)}{f(X|\omega_1)} </math> | ||
| Line 26: | Line 25: | ||
== 贝叶斯(Bayes)判决规则 == | == 贝叶斯(Bayes)判决规则 == | ||
| − | <span class="texhtml">''g''<sub>''i''</sub>(''X'')</span> 是<span class="texhtml">ω<sub>''i''</sub></span>的'''后验概率(posterior probability)'''。选<span class="texhtml">ω<sub>1</sub></span>或<span class="texhtml">ω<sub>2</sub></span>的判决规则为: 如果<span class="texhtml">''g''<sub>0</sub>(''X'') > ''g''<sub>1</sub>(''X'')</span>,就选<span class="texhtml">ω<sub>0</sub></span>, 不然选<span class="texhtml">ω<sub>1</sub></span> | + | <span class="texhtml">''g''<sub>''i''</sub>(''X'')</span> 是<span class="texhtml">ω<sub>''i''</sub></span>的'''后验概率(posterior probability)'''。选<span class="texhtml">ω<sub>1</sub></span>或<span class="texhtml">ω<sub>2</sub></span>的判决规则为: 如果<span class="texhtml">''g''<sub>0</sub>(''X'') > ''g''<sub>1</sub>(''X'')</span>,就选<span class="texhtml">ω<sub>0</sub></span>, 不然选<span class="texhtml">ω<sub>1</sub></span>。据贝叶斯定理, 判决规则能以 '''似然比(likelihood ratio)'''表示: |
<math>\begin{align} | <math>\begin{align} | ||
& g_0(X) > g_1(X) \\ | & g_0(X) > g_1(X) \\ | ||
\Rightarrow & P(\omega_0|X) > P(\omega_1|X) \\ | \Rightarrow & P(\omega_0|X) > P(\omega_1|X) \\ | ||
| − | \Rightarrow & \frac{f(X|\omega_0)P(\omega_0)}{ | + | \Rightarrow & \frac{f(X|\omega_0)P(\omega_0)}{f(X)} > \frac{f(X|\omega_1)P(\omega_1)}{f(X)} \\ |
\Rightarrow & f(X|\omega_0)P(\omega_0) > f(X|\omega_1)P(\omega_1) \\ | \Rightarrow & f(X|\omega_0)P(\omega_0) > f(X|\omega_1)P(\omega_1) \\ | ||
\Rightarrow & l(X) = \frac{f(X|\omega_0)}{f(X|\omega_1)} > \frac{P(\omega_1)}{P(\omega_0)} = k | \Rightarrow & l(X) = \frac{f(X|\omega_0)}{f(X|\omega_1)} > \frac{P(\omega_1)}{P(\omega_0)} = k | ||
| Line 37: | Line 36: | ||
</math> | </math> | ||
| − | + | 贝叶斯判决规则就说明可以通过似然比与常数的比较进行决定,叫做'''似然比检测(likelihood ratio test)'''。 | |
== 贝叶斯错误 == | == 贝叶斯错误 == | ||
| Line 51: | Line 50: | ||
\begin{align} | \begin{align} | ||
\\ | \\ | ||
| − | \epsilon_{Bayes} & = E(r(X)) = \int min(P(\omega_0) | + | \epsilon_{Bayes} & = E(r(X)) = \int min(P(\omega_0)f(X|\omega_0), P(\omega_1)f(X|\omega_1))dX \\ |
| − | &= P(\omega_0) \int_{R_1} | + | &= P(\omega_0) \int_{R_1}f(X|\omega_0)dX + P(\omega_1) \int_{R_0} f(X|\omega_1)dX \\ |
&= P(\omega_0)\epsilon_0 + P(\omega_1)\epsilon_1 | &= P(\omega_0)\epsilon_0 + P(\omega_1)\epsilon_1 | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
| − | == | + | == Neyman-Pearson引理 == |
| − | + | 统计学中的假设检验有个概念叫做“一致最大功效检验(UMP test)”。UMP 的检验满足一个条件:定义为在固定一种错误率的同时尽可能减少另一种错误率的检验。 | |
| − | <blockquote> | + | |
| + | Neyman-Pearson引理:决定规则当UMP test的充分必要条件如下: | ||
| + | <blockquote> | ||
<br> | <br> | ||
| − | + | *ε<sub>0</sub>被固定在一位常数α然后决定规则是 | |
| − | <br> | + | *如果<br> |
| − | + | <math> l(X)=\frac{f(X| \omega_0 )}{f(X| \omega_1)} > k </math><br> | |
| + | 决定选<math> \omega_0 </math> | ||
| + | *如果<br> | ||
| + | <math> l(X)=\frac{f(X| \omega_0 )}{f(X|\omega_1 )} < k </math><br> | ||
| + | 决定选<math> \omega_1 </math>。 | ||
| + | </blockquote> | ||
| + | |||
| + | |||
| + | ==例子:统计学假设检验<br> == | ||
| + | |||
| + | 如果你曾经上过入门的统计学课,你大概能想起传统的假设检验. 如下为例子: <br> | ||
| + | <blockquote>一位人类学研究者争对一个太平岛的部落做出一个假设:此部落预期寿命比一般人长。全世界人口的预期寿命是67.2年。为了检验他的假设,他从公开记录中随机选出了100个讣告作为样本,发现样本平均预期寿命是72,标准差是15。为了保守,这位研究者不轻易接受他的假设。他知道他的样本是随机变量,即使样本和人口的差别很大,但有可能这个差别来自随机性。他想控制由于随机性错误接受他的假设的概率保证不超越.05.</blockquote> | ||
<br> | <br> | ||
| − | |||
| − | |||
| − | |||
| − | + | === 似然比检验 === | |
| − | + | 这个例子完全可以用模式识别的语言来描述。为了达到简单的计算。。。 | |
| + | # 假设似然函数是正常分布(Normal Distribution) | ||
| + | # 不用全部100人的似然函数,而直接用充分统计量--就是样本平均值--的似然函数,此函数也是正常分布 | ||
| + | # 把样本平均值的函数标准化(标准差=1)。 | ||
| − | |||
| − | + | 把 <span class="texhtml">μ</span> 定义为此部落预期寿命。 | |
| + | 零假设 (ω<sub>0</sub>): <span class="texhtml">μ − 67.2 = 0</span> | ||
| + | <br> | ||
| + | 对立假设(ω<sub>1</sub>): <span class="texhtml">μ − 67.2 > 0</span> | ||
| + | <br> | ||
| − | + | 把样本的100人的数据变成样本平均值“T”(等于T就是我们的特征向量)。如果ω<sub>0</sub>是正确,此部落的平均值是全世界人口的平均值。样本的平均值“T”就是随机差别,等于f(T|ω<sub>0</sub>)是正常分布(平均数是67.2,标准差是15)。如果ω<sub>1</sub>,部落的平均不一样。他的正常分布的平均值就跟全世界平均值不一样。由于我们在考虑似然函数,可以用此平均值的MLE--就是样本的平均值--,所以f(T|ω<sub>1</sub>)是正常分布(平均数是72,标准差是15)。最后用f(T|ω<sub>0</sub>)的平均值把两分布标准化。把φ(x; a,b)定义为平均值等于a标准差等于b的标正常分布的PDF。<br> | |
| + | z =(t - 67.2)/(15 * 15 / 100) = (72 - 67.2)/(15 * 15 / 100) = 2<br> | ||
| + | f(T = 72|ω<sub>0</sub>) = φ(2; 0, 1) <br> | ||
| + | f(T = 72|ω<sub>1</sub>) = φ(2; 2, 1) <br> | ||
| + | <math> | ||
| + | \frac{f(t|\omega_0)}{f(t|\omega_1)} = \frac{\phi(2;0,1)}{\phi(2;2,1)} = \frac{exp(-2^2/2))}{exp(0)}=exp(-2^2/2)=0.1353 | ||
| + | </math> | ||
| + | <br> | ||
| − | + | ''' 控制错误率 ''' | |
| − | + | 我们的研究者要保证P(决定ω<sub>1</sub>) | ω<sub>1</sub>)正确)=ε<sub>0</sub> 不超越.05. | |
| − | + | ||
| − | + | ||
| − | |||
<blockquote> | <blockquote> | ||
<br> | <br> | ||
| − | *ε<sub>0</sub> | + | *ε<sub>0</sub><.05 |
*如果<br> | *如果<br> | ||
| − | <math> l( | + | <math> l(t)=\frac{f(t| \omega_0 )}{f(t| \omega_1)} > k </math><br> |
决定选<math> \omega_0 </math> | 决定选<math> \omega_0 </math> | ||
*如果<br> | *如果<br> | ||
| − | <math> l( | + | <math> l(t)=\frac{f(t| \omega_0 )}{f(t|\omega_1 )} < k </math><br> |
决定选<math> \omega_1 </math>。 | 决定选<math> \omega_1 </math>。 | ||
</blockquote> | </blockquote> | ||
| + | <br> | ||
| + | 我们要找出满足这些条件的k。为了找到k,我们需要找个判决界限“z<sub>.05</sub>“: | ||
| + | <br> | ||
| + | <math> | ||
| + | k= \frac{\phi(z_c;0,1)}{\phi(z;2,1)}=exp(-z_c^2/2) | ||
| + | </math> | ||
| + | <br> | ||
| + | 由此得出。。。: | ||
| + | <br> | ||
| + | <math> | ||
| + | \epsilon_0 = \int_{R_1} f(t|\omega_0)dt = \int_{z_c}^{\infty}\phi(z;0,1)dz \leq .05 | ||
| + | </math> | ||
| + | <br> | ||
| + | 为了找到k,要把此不等变成方程式:<br> | ||
| + | <br> | ||
| + | <math> | ||
| + | \epsilon_0 = \int_{R_1} f(t|\omega_0)dt = \int_{z_c}^{\infty}\phi(z;0,1)dz = .05 | ||
| + | </math> | ||
| + | <br> | ||
| + | 然后,把两边从1剪掉。。。: | ||
| + | <br> | ||
| + | <math> | ||
| + | \int_{\infty}^{z_c}\phi(z;0,1)dz = .95 | ||
| + | </math> | ||
| + | <br> | ||
| + | 用Matlab或者正常分布表格,就得出z<sub>c</sub>等于1.644. 结果 k = exp(-1.644^2/2) = 0.259 | ||
| + | <br> | ||
| + | 我们得出的l(t)是0.1353 < k = 0.259,所按照我们的判决规则,决定ω<sub>1</sub>。 | ||
| + | |||
| + | '''约束先验概率(Prior)''' | ||
| + | 从这个分析得出一个很重要的结论:控制一类的错误等于决定先验概率: | ||
| + | <br> | ||
| + | <math> | ||
| + | \begin{align}\\ | ||
| + | .259 = k &= \frac{P(\omega_1)}{P(w_0)}\\ | ||
| + | P(\omega_1)&=P(\omega_0)k\\ | ||
| + | 1-P(\omega_0)&=P(\omega_0)k\\ | ||
| + | P(\omega_0)(1+k) &=1\\ | ||
| + | P(\omega_0)&=1/(1+k) = 0.794\\ | ||
| + | P(\omega_1) &= 0.206 | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | <br> | ||
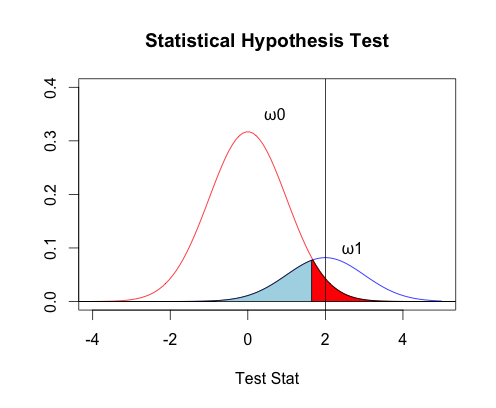
| + | 有了先验概率之后,可以画g<sub>0</sub>(t)=f(t|ω<sub>0</sub>)P(ω<sub>0</sub>)与g<sub>1</sub>(t)=f(t|ω<sub>1</sub>)P(ω<sub>1</sub>)的曲线: | ||
| + | |||
| + | '''[[Image:Rplot01.png]]''' | ||
| + | |||
| + | 蓝色的领域是ε<sub>1</sub>、粉红色的领域是ε<sub>0</sub>。因为判决界限在1.644然后t=2,所以选ω<sub>1</sub>。界限在g<sub>1</sub>(t)-g<sub>0</sub>(t)的根,所以错误率是尽可能减少。这个图表明约束了ε<sub>0</sub>之后,ε<sub>1</sub>还是尽可能少了。 | ||
==结论== | ==结论== | ||
| − | + | ||
| + | 贝叶斯的判决规则可以用似然比来表达。由此,Newman-Pearson引理说如果我们想控制一类的错误率,同时可以尽可能减少另一类的错误率。上面的例子用了统计学假设检验的例子。研究者想把ε<sub>0</sub>控制在.05以下。这个条件通过Newman-Pearson引理得出一个k。这个k决定先验概率,用先验概率就有g<sub>0</sub>(t)与g<sub>1</sub>(t).检查这两函数就发现依然有贝叶斯的错误率,等于ε<sub>1</sub>是尽可能少了。 | ||
| + | |||
== References == | == References == | ||
Latest revision as of 09:46, 22 January 2015
Neyman-Pearson: How Bayes Decision Rule Controls Error
A slecture by Robert Ness
Partly based on the ECE662 Spring 2014 lecture material of Prof. Mireille Boutin.
Contents
介绍
模式识别 的目标是将新观察的特征向量进行分类。为了进行分类的决定,需要通过某种判决规则(decision rule)。在 统计学模式识别 一般假设特征向量是个随机变量“X”,又有个概率密度函数或者概率质量函数,并且此函数依赖其分类。假设有两个类型:(ω0,ω1), 以便写公式也不会失去一般性。X的概率密度或质量函数是f(X | ωi) (如下称pdf)。每个类型的先验概率写成P(ωi)。
两类问题有两种错误:错误选第一类、错误选第二类。下面说明(1)如果用贝叶斯(Bayes)判决规则,等于做似然比检验 (Likelihood Ratio Test),加上(2)Neyman-Pearson引理证明由于在用似然比检验,判决规则能控制一种错误率在一定的数量的同时将另一类的错误率控制在尽可能最少的数量。下面用统计学假设检验(Statistical Hypothesis Test)和标准正常分布(Standard Normal Distribution)作为例子。
似然比检验
似然比统计定义为:
$ \lambda(X)=\frac{f(X|\omega_0)}{f(X|\omega_1)} $
似然比检验定义为:
如果
$ \lambda(X) > k $
。。。决定ω0,不然决定ω1,∀ k:0 < k < 1
贝叶斯(Bayes)判决规则
gi(X) 是ωi的后验概率(posterior probability)。选ω1或ω2的判决规则为: 如果g0(X) > g1(X),就选ω0, 不然选ω1。据贝叶斯定理, 判决规则能以 似然比(likelihood ratio)表示:
$ \begin{align} & g_0(X) > g_1(X) \\ \Rightarrow & P(\omega_0|X) > P(\omega_1|X) \\ \Rightarrow & \frac{f(X|\omega_0)P(\omega_0)}{f(X)} > \frac{f(X|\omega_1)P(\omega_1)}{f(X)} \\ \Rightarrow & f(X|\omega_0)P(\omega_0) > f(X|\omega_1)P(\omega_1) \\ \Rightarrow & l(X) = \frac{f(X|\omega_0)}{f(X|\omega_1)} > \frac{P(\omega_1)}{P(\omega_0)} = k \end{align} $
贝叶斯判决规则就说明可以通过似然比与常数的比较进行决定,叫做似然比检测(likelihood ratio test)。
贝叶斯错误
为了评估判决规则的效果,需要计算错误的概率。计算需要如下的记法定义:
- $ \epsilon_0 $ = P(错误选ω1 | ω0正确),$ \epsilon_1 $ = P(错误选ω0 | ω1正确)
- Ri是选ωi的领域:
$ R_i=\{x\in X | choose \ \omega_i\} $
- r(X)= min(g0(X),g1(X))。
在贝叶斯决定规则下,错误几率等于贝叶斯错误几率(Bayes error rate):
$ \begin{align} \\ \epsilon_{Bayes} & = E(r(X)) = \int min(P(\omega_0)f(X|\omega_0), P(\omega_1)f(X|\omega_1))dX \\ &= P(\omega_0) \int_{R_1}f(X|\omega_0)dX + P(\omega_1) \int_{R_0} f(X|\omega_1)dX \\ &= P(\omega_0)\epsilon_0 + P(\omega_1)\epsilon_1 \end{align} $
Neyman-Pearson引理
统计学中的假设检验有个概念叫做“一致最大功效检验(UMP test)”。UMP 的检验满足一个条件:定义为在固定一种错误率的同时尽可能减少另一种错误率的检验。
Neyman-Pearson引理:决定规则当UMP test的充分必要条件如下:
- ε0被固定在一位常数α然后决定规则是
- 如果
$ l(X)=\frac{f(X| \omega_0 )}{f(X| \omega_1)} > k $
决定选$ \omega_0 $
- 如果
$ l(X)=\frac{f(X| \omega_0 )}{f(X|\omega_1 )} < k $
决定选$ \omega_1 $。
例子:统计学假设检验
如果你曾经上过入门的统计学课,你大概能想起传统的假设检验. 如下为例子:
一位人类学研究者争对一个太平岛的部落做出一个假设:此部落预期寿命比一般人长。全世界人口的预期寿命是67.2年。为了检验他的假设,他从公开记录中随机选出了100个讣告作为样本,发现样本平均预期寿命是72,标准差是15。为了保守,这位研究者不轻易接受他的假设。他知道他的样本是随机变量,即使样本和人口的差别很大,但有可能这个差别来自随机性。他想控制由于随机性错误接受他的假设的概率保证不超越.05.
似然比检验
这个例子完全可以用模式识别的语言来描述。为了达到简单的计算。。。
- 假设似然函数是正常分布(Normal Distribution)
- 不用全部100人的似然函数,而直接用充分统计量--就是样本平均值--的似然函数,此函数也是正常分布
- 把样本平均值的函数标准化(标准差=1)。
把 μ 定义为此部落预期寿命。
零假设 (ω0): μ − 67.2 = 0
对立假设(ω1): μ − 67.2 > 0
把样本的100人的数据变成样本平均值“T”(等于T就是我们的特征向量)。如果ω0是正确,此部落的平均值是全世界人口的平均值。样本的平均值“T”就是随机差别,等于f(T|ω0)是正常分布(平均数是67.2,标准差是15)。如果ω1,部落的平均不一样。他的正常分布的平均值就跟全世界平均值不一样。由于我们在考虑似然函数,可以用此平均值的MLE--就是样本的平均值--,所以f(T|ω1)是正常分布(平均数是72,标准差是15)。最后用f(T|ω0)的平均值把两分布标准化。把φ(x; a,b)定义为平均值等于a标准差等于b的标正常分布的PDF。
z =(t - 67.2)/(15 * 15 / 100) = (72 - 67.2)/(15 * 15 / 100) = 2
f(T = 72|ω0) = φ(2; 0, 1)
f(T = 72|ω1) = φ(2; 2, 1)
$ \frac{f(t|\omega_0)}{f(t|\omega_1)} = \frac{\phi(2;0,1)}{\phi(2;2,1)} = \frac{exp(-2^2/2))}{exp(0)}=exp(-2^2/2)=0.1353 $
控制错误率
我们的研究者要保证P(决定ω1) | ω1)正确)=ε0 不超越.05.
- ε0<.05
- 如果
$ l(t)=\frac{f(t| \omega_0 )}{f(t| \omega_1)} > k $
决定选$ \omega_0 $
- 如果
$ l(t)=\frac{f(t| \omega_0 )}{f(t|\omega_1 )} < k $
决定选$ \omega_1 $。
我们要找出满足这些条件的k。为了找到k,我们需要找个判决界限“z.05“:
$ k= \frac{\phi(z_c;0,1)}{\phi(z;2,1)}=exp(-z_c^2/2) $
由此得出。。。:
$ \epsilon_0 = \int_{R_1} f(t|\omega_0)dt = \int_{z_c}^{\infty}\phi(z;0,1)dz \leq .05 $
为了找到k,要把此不等变成方程式:
$ \epsilon_0 = \int_{R_1} f(t|\omega_0)dt = \int_{z_c}^{\infty}\phi(z;0,1)dz = .05 $
然后,把两边从1剪掉。。。:
$ \int_{\infty}^{z_c}\phi(z;0,1)dz = .95 $
用Matlab或者正常分布表格,就得出zc等于1.644. 结果 k = exp(-1.644^2/2) = 0.259
我们得出的l(t)是0.1353 < k = 0.259,所按照我们的判决规则,决定ω1。
约束先验概率(Prior)
从这个分析得出一个很重要的结论:控制一类的错误等于决定先验概率:
$ \begin{align}\\ .259 = k &= \frac{P(\omega_1)}{P(w_0)}\\ P(\omega_1)&=P(\omega_0)k\\ 1-P(\omega_0)&=P(\omega_0)k\\ P(\omega_0)(1+k) &=1\\ P(\omega_0)&=1/(1+k) = 0.794\\ P(\omega_1) &= 0.206 \end{align} $
有了先验概率之后,可以画g0(t)=f(t|ω0)P(ω0)与g1(t)=f(t|ω1)P(ω1)的曲线:
蓝色的领域是ε1、粉红色的领域是ε0。因为判决界限在1.644然后t=2,所以选ω1。界限在g1(t)-g0(t)的根,所以错误率是尽可能减少。这个图表明约束了ε0之后,ε1还是尽可能少了。
结论
贝叶斯的判决规则可以用似然比来表达。由此,Newman-Pearson引理说如果我们想控制一类的错误率,同时可以尽可能减少另一类的错误率。上面的例子用了统计学假设检验的例子。研究者想把ε0控制在.05以下。这个条件通过Newman-Pearson引理得出一个k。这个k决定先验概率,用先验概率就有g0(t)与g1(t).检查这两函数就发现依然有贝叶斯的错误率,等于ε1是尽可能少了。
References
- Mireille Boutin, "ECE662: Statistical Pattern Recognition and Decision Making Processes," Purdue University, Spring 2014.
- Casella, George, and Roger L. Berger. Statistical inference. Vol. 70. Belmont, CA: Duxbury Press, 1990.
- Fukunaga, Keinosuke. Introduction to statistical pattern recognition. Academic press, 1990.
Questions and comments
If you have any questions, comments, etc. please post them On this page.