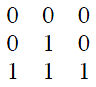| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
[[Category:2010 Fall ECE 438 Boutin]] | [[Category:2010 Fall ECE 438 Boutin]] | ||
| + | [[Category:Problem_solving]] | ||
| + | [[Category:ECE438]] | ||
| + | [[Category:digital signal processing]] | ||
| + | |||
== Quiz Questions Pool for Week 14 == | == Quiz Questions Pool for Week 14 == | ||
---- | ---- | ||
| Line 37: | Line 41: | ||
c. Find a simple expression for the frequency response (DSFT) H(u,v) of this filter. | c. Find a simple expression for the frequency response (DSFT) H(u,v) of this filter. | ||
| − | |||
| − | |||
* [[ECE438_Week14_Quiz_Q3sol|Solution]]. | * [[ECE438_Week14_Quiz_Q3sol|Solution]]. | ||
| Line 52: | Line 54: | ||
* [[ECE438_Week14_Quiz_Q4sol|Solution]]. | * [[ECE438_Week14_Quiz_Q4sol|Solution]]. | ||
---- | ---- | ||
| + | Q5. Consider the following discrete space system | ||
| + | [[Image:Quiz14Q5.jpg]] | ||
| + | |||
| + | where <math>b(i,j)</math> is the quantized binary image, <math>f(i,j)</math> is the input and <math>\tilde{f}(i,j)</math> is the modified image by means of the past quantization errors. | ||
| + | |||
| + | Furthermore we have that | ||
| + | :<math>\begin{align}e(i,j)&=\tilde{f}(i,j)-b(i,j) \\ \tilde{f}(i,j)&=f(i,j)+H(i,j)\ast e(i,j) \\ \end{align}</math> | ||
| + | |||
| + | Now, we have <math>H(i,j)=\delta(i-1,j)\,\!</math> is a strictly causal filter and the quantizer <math>Q(\tilde{f})</math> given as | ||
| + | :<math>Q(\tilde{f})=\left\{ \begin{array}{ll}1,& \tilde{f}(i,j)>0.5 \\ 0, & \tilde{f}(i,j)\leq 0.5 \end{array} \right. </math> | ||
| + | |||
| + | Assuming that <math>e(i,j)=0</math> for <math>i<0</math> and <math>j<0</math> and the input <math>f(i,j)</math> to be defined as | ||
| + | |||
| + | [[Image:Quiz14Q5_1.jpg]] | ||
| + | |||
| + | a. compute the modified input <math>\tilde{f}(i,j)</math>. | ||
| + | |||
| + | [[Image:Quiz14Q5_2.jpg]] | ||
| + | |||
| + | b. compute the output <math>b(i,j)</math>. | ||
| + | |||
| + | [[Image:Quiz14Q5_3.jpg]] | ||
| + | |||
| + | * [[ECE438_Week14_Quiz_Q5sol|Solution]]. | ||
| + | ---- | ||
Back to [[ECE438_Lab_Fall_2010|ECE 438 Fall 2010 Lab Wiki Page]] | Back to [[ECE438_Lab_Fall_2010|ECE 438 Fall 2010 Lab Wiki Page]] | ||
Back to [[2010_Fall_ECE_438_Boutin|ECE 438 Fall 2010]] | Back to [[2010_Fall_ECE_438_Boutin|ECE 438 Fall 2010]] | ||
Latest revision as of 09:43, 11 November 2011
Quiz Questions Pool for Week 14
Q1. Assume we know (or can measure) a function
$ \begin{align} p(x) &= \int_{-\infty}^{\infty}f(x,y)dy \end{align} $
Using the definition of the CSFT, derive an expression for F(u,0) in terms of the function p(x).
Q2. Consider the following 2D system with input x(m,n) and output y(m,n)
$ y(m,n) = x(m,n) + \lambda \left( x(m,n) - \frac{1}{9} \sum_{k=-1}^{1}\sum_{l=-1}^{1}x(m-k,n-l) \right) $
a. Is this a linear system? Is it space invariant?
b. What is the 2D impulse response of this system?
c. Calculate its frequency response H(u,v).
d. Describe how the filter behaves when $ \lambda $ is positive and large.
e. Describe how the filter behaves when $ \lambda $ is negative and bigger than -1.
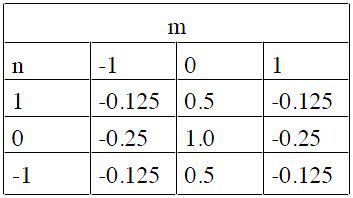
Q3. Consider a 3 * 3 FIR filter with coefficients h[m, n]
a. Find a difference equation that can be used to implement this filter.
b. Given an input image, find the center pixel value of output image.
c. Find a simple expression for the frequency response (DSFT) H(u,v) of this filter.
Q4. Consider the following discrete space system with input x[m,n] and output y[m,n]given by
$ y[m,n]=x[m,n]+\frac{1}{2}y[m+1,n-1] $
Compute the transfer function
$ H(z_1 ,z_2)=\frac{Y(z_1 ,z_2)}{X(z_1 ,z_2)} $
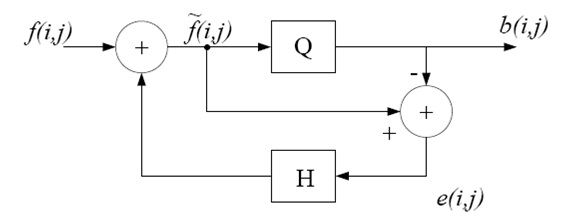
Q5. Consider the following discrete space system
where $ b(i,j) $ is the quantized binary image, $ f(i,j) $ is the input and $ \tilde{f}(i,j) $ is the modified image by means of the past quantization errors.
Furthermore we have that
- $ \begin{align}e(i,j)&=\tilde{f}(i,j)-b(i,j) \\ \tilde{f}(i,j)&=f(i,j)+H(i,j)\ast e(i,j) \\ \end{align} $
Now, we have $ H(i,j)=\delta(i-1,j)\,\! $ is a strictly causal filter and the quantizer $ Q(\tilde{f}) $ given as
- $ Q(\tilde{f})=\left\{ \begin{array}{ll}1,& \tilde{f}(i,j)>0.5 \\ 0, & \tilde{f}(i,j)\leq 0.5 \end{array} \right. $
Assuming that $ e(i,j)=0 $ for $ i<0 $ and $ j<0 $ and the input $ f(i,j) $ to be defined as
a. compute the modified input $ \tilde{f}(i,j) $.
b. compute the output $ b(i,j) $.
Back to ECE 438 Fall 2010 Lab Wiki Page
Back to ECE 438 Fall 2010