(New page: Category:2010 Fall ECE 438 Boutin ---- == Quiz Questions Pool for Week 9 == ---- Q1. * Solution. ---- Q2. * Solution. ---- ...) |
|||
| (14 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
[[Category:2010 Fall ECE 438 Boutin]] | [[Category:2010 Fall ECE 438 Boutin]] | ||
| − | + | [[Category:Problem_solving]] | |
| + | [[Category:ECE438]] | ||
| + | [[Category:digital signal processing]] | ||
---- | ---- | ||
== Quiz Questions Pool for Week 9 == | == Quiz Questions Pool for Week 9 == | ||
---- | ---- | ||
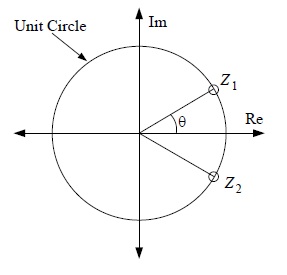
| − | Q1. | + | Q1. Consider the following second order FIR filter with the two zeros on the unit circle as shown below. |
| + | |||
| + | [[Image:Quiz9Q1.jpg]] | ||
| + | |||
| + | The transfer function for this filter is given by <math> H(z) = (1-e^{j\theta}z^{-1})(1-e^{-j\theta}z^{-1})=1-2\cos\theta z^{-1}+z^{-2}</math> | ||
| + | |||
| + | :a. Find the difference equation of this filter. | ||
| + | |||
| + | :b. Find the frequency response <math>H(w)</math> from the difference equation by the following two approaches: | ||
| + | ::i. apply the input <math>e^{jwn}</math> to the difference equation describing the system, | ||
| + | ::ii. find the DTFT of the impulse response, | ||
| + | : and verify that both methods lead to the same result. | ||
| + | |||
| + | :c. Find the response of this system to the input | ||
| + | ::<math> | ||
| + | x[n]=\left\{ | ||
| + | \begin{array}{rl} | ||
| + | 1, & \text{ if }n=-1,\\ | ||
| + | 1, & \text{ if }n=0,\\ | ||
| + | 0, & \text{ else. } | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </math> | ||
| + | |||
| + | :d. When <math>\theta=\pi/2</math>, is this filter a lowpass, highpass, bandpass or a bandstop filter? | ||
| + | |||
| + | :e. An interference signal modulated at 2kHz and sampled at 8kHz is being inputted to this system and you want to eliminate this interference. What must be the value of <math>\theta</math> to eliminate this signal? | ||
* [[ECE438_Week9_Quiz_Q1sol|Solution]]. | * [[ECE438_Week9_Quiz_Q1sol|Solution]]. | ||
---- | ---- | ||
| − | Q2. | + | Q2. When we have a LTI system, the impulse response <math>h[n]</math> must be real |
| + | |||
| + | in order for <math>y[n]</math> to be real whenever <math>x[n]</math> is real. | ||
| + | |||
| + | The condition for <math>h[n]</math> to be real is | ||
| + | |||
| + | <math> h[n]=h^{\ast}[n] </math> | ||
| + | |||
| + | Then, what is the condition of the frequency response <math>H(w)</math> for <math>h[n]</math> to be real? | ||
| + | |||
| + | (Hint: Apply DTFT to the above equation) | ||
* [[ECE438_Week9_Quiz_Q2sol|Solution]]. | * [[ECE438_Week9_Quiz_Q2sol|Solution]]. | ||
| + | ---- | ||
| + | Q3. | ||
| + | |||
| + | Consider a DT LTI system described by the following equation | ||
| + | |||
| + | <math>y[n] = x[n] + 2x[n - 1] + 0.5y[n - 1] </math> | ||
| + | |||
| + | a. Compute the impulse response h[n] of the system. <br/> | ||
| + | b. Compute the output when x[n] = u[n]. <br/> | ||
| + | c. Compute the output when <math>x[n] = 0.25^nu[n]</math>. <br/> | ||
| + | |||
| + | * [[ECE438_Week9_Quiz_Q3sol|Solution]]. | ||
| + | ---- | ||
| + | Q4. | ||
| + | |||
| + | Given the difference equation of the system: | ||
| + | |||
| + | <math>y[n]=\frac{1}{M_1+M_2+1}\sum_{k=-M_1}^{M_2}x[n-k]\text{ ,}M_1,M_2\ge 0</math> | ||
| + | |||
| + | a. Compute the impulse response of the system h[n] | ||
| + | |||
| + | b. Compute the frequency response of <math>H(e^{jw})</math>. | ||
| + | |||
| + | c. Suppose <math>M_1=0,M_2=4</math>. Sketch the magnitude of <math>H(e^{jw})</math> on the interval <math>[-\pi ,\pi]</math> | ||
| + | |||
| + | |||
| + | * [[ECE438_Week9_Quiz_Q4sol|Solution]]. | ||
| + | ---- | ||
| + | Q5. | ||
| + | |||
| + | Obtain the Duality Property of DFT. | ||
| + | |||
| + | * [[ECE438_Week9_Quiz_Q5sol|Solution]]. | ||
---- | ---- | ||
Latest revision as of 09:42, 11 November 2011
Quiz Questions Pool for Week 9
Q1. Consider the following second order FIR filter with the two zeros on the unit circle as shown below.
The transfer function for this filter is given by $ H(z) = (1-e^{j\theta}z^{-1})(1-e^{-j\theta}z^{-1})=1-2\cos\theta z^{-1}+z^{-2} $
- a. Find the difference equation of this filter.
- b. Find the frequency response $ H(w) $ from the difference equation by the following two approaches:
- i. apply the input $ e^{jwn} $ to the difference equation describing the system,
- ii. find the DTFT of the impulse response,
- and verify that both methods lead to the same result.
- c. Find the response of this system to the input
- $ x[n]=\left\{ \begin{array}{rl} 1, & \text{ if }n=-1,\\ 1, & \text{ if }n=0,\\ 0, & \text{ else. } \end{array} \right. $
- d. When $ \theta=\pi/2 $, is this filter a lowpass, highpass, bandpass or a bandstop filter?
- e. An interference signal modulated at 2kHz and sampled at 8kHz is being inputted to this system and you want to eliminate this interference. What must be the value of $ \theta $ to eliminate this signal?
Q2. When we have a LTI system, the impulse response $ h[n] $ must be real
in order for $ y[n] $ to be real whenever $ x[n] $ is real.
The condition for $ h[n] $ to be real is
$ h[n]=h^{\ast}[n] $
Then, what is the condition of the frequency response $ H(w) $ for $ h[n] $ to be real?
(Hint: Apply DTFT to the above equation)
Q3.
Consider a DT LTI system described by the following equation
$ y[n] = x[n] + 2x[n - 1] + 0.5y[n - 1] $
a. Compute the impulse response h[n] of the system.
b. Compute the output when x[n] = u[n].
c. Compute the output when $ x[n] = 0.25^nu[n] $.
Q4.
Given the difference equation of the system:
$ y[n]=\frac{1}{M_1+M_2+1}\sum_{k=-M_1}^{M_2}x[n-k]\text{ ,}M_1,M_2\ge 0 $
a. Compute the impulse response of the system h[n]
b. Compute the frequency response of $ H(e^{jw}) $.
c. Suppose $ M_1=0,M_2=4 $. Sketch the magnitude of $ H(e^{jw}) $ on the interval $ [-\pi ,\pi] $
Q5.
Obtain the Duality Property of DFT.
Back to ECE 438 Fall 2010 Lab Wiki Page
Back to ECE 438 Fall 2010