| (3 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
Most patterns that we come across in everyday life are examples of periodic tiling. On the surface, these patterns (also called '''tessellations''') attract attention for their appearance, since patterns are easy to duplicate and have an aesthetic design once complete. This can be seen in both nature and man-made structures: flowers often contain never-ending spirals and symmetrical petals, and repetitive patterns often show up as decorations in quilts, building floors, and ceramic artwork. | Most patterns that we come across in everyday life are examples of periodic tiling. On the surface, these patterns (also called '''tessellations''') attract attention for their appearance, since patterns are easy to duplicate and have an aesthetic design once complete. This can be seen in both nature and man-made structures: flowers often contain never-ending spirals and symmetrical petals, and repetitive patterns often show up as decorations in quilts, building floors, and ceramic artwork. | ||
| − | But some may argue that the real intrinsic beauty of these patterns is their applications to math and science. Regarding biochemistry, “ordered and periodic” structures have been found in crystalline structures[https://www.goldennumber.net/quasi-crystals/]. In nature, bees create honeycomb structures for efficient construction | + | <center> |
| + | [[File:Flower petals golden ratio.jpg|frame|300x250px|Flower petals naturally following the golden ratio]] <br> | ||
| + | <small> [https://en.wikipedia.org/wiki/Golden_ratio#Nature Wikipedia] </small> | ||
| + | </center> | ||
| + | |||
| + | But some may argue that the real intrinsic beauty of these patterns is their applications to math and science. Regarding biochemistry, “ordered and periodic” structures have been found in crystalline structures[https://www.goldennumber.net/quasi-crystals/]. In nature, bees create honeycomb structures for efficient construction — multiple bees can work on different cells at once and meet in the middle. The hexagons have a larger area but the same perimeter as a triangular tessellation, which means less beeswax is used and the overall honeycomb has more storage space. | ||
To put it simply, periodic means something repeats (think of a trigonometric function like sine, which has a period of 2<math> \pi </math>). So periodic tiling has a repeated pattern throughout a plane. On the other hand, aperiodic tiling does not have a predictable pattern, even on an infinite plane. The latter category is where Penrose tiling fall into. | To put it simply, periodic means something repeats (think of a trigonometric function like sine, which has a period of 2<math> \pi </math>). So periodic tiling has a repeated pattern throughout a plane. On the other hand, aperiodic tiling does not have a predictable pattern, even on an infinite plane. The latter category is where Penrose tiling fall into. | ||
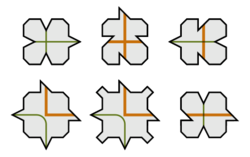
| − | The earliest known interest in aperiodic tiling is the logician Hao Wang’s aperiodic set. In the 1960s Wang came up with the Domino Problem, which involved his set of Wang dominoes (also called '''tiles''') and tried to determine if those dominoes could be matched together by the colors on the edges of the dominoes without rotating the dominoes | + | The earliest known interest in aperiodic tiling is the logician Hao Wang’s aperiodic set. In the 1960s Wang came up with the Domino Problem, which involved his set of Wang dominoes (also called '''tiles''') and tried to determine if those dominoes could be matched together by the colors on the edges of the dominoes without rotating the dominoes — a technique that resembles how one would complete a jigsaw puzzle. If this were impossible, that would mean an aperiodic tiling could be made with a set of Wang dominoes. At the time, Wang thought the problem was solvable (therefore no set of aperiodic Wang dominoes could exist), but over the years, other mathematicians — including his student — proved him wrong and created simpler and simpler aperiodic sets of Wang dominoes. Finally, in 1971, Raphael Robinson used the same technique to achieve a set of just six aperiodic tiles (pictured below). |
<center> | <center> | ||
Latest revision as of 22:16, 6 December 2020
Introduction
Most patterns that we come across in everyday life are examples of periodic tiling. On the surface, these patterns (also called tessellations) attract attention for their appearance, since patterns are easy to duplicate and have an aesthetic design once complete. This can be seen in both nature and man-made structures: flowers often contain never-ending spirals and symmetrical petals, and repetitive patterns often show up as decorations in quilts, building floors, and ceramic artwork.
But some may argue that the real intrinsic beauty of these patterns is their applications to math and science. Regarding biochemistry, “ordered and periodic” structures have been found in crystalline structures[1]. In nature, bees create honeycomb structures for efficient construction — multiple bees can work on different cells at once and meet in the middle. The hexagons have a larger area but the same perimeter as a triangular tessellation, which means less beeswax is used and the overall honeycomb has more storage space.
To put it simply, periodic means something repeats (think of a trigonometric function like sine, which has a period of 2$ \pi $). So periodic tiling has a repeated pattern throughout a plane. On the other hand, aperiodic tiling does not have a predictable pattern, even on an infinite plane. The latter category is where Penrose tiling fall into.
The earliest known interest in aperiodic tiling is the logician Hao Wang’s aperiodic set. In the 1960s Wang came up with the Domino Problem, which involved his set of Wang dominoes (also called tiles) and tried to determine if those dominoes could be matched together by the colors on the edges of the dominoes without rotating the dominoes — a technique that resembles how one would complete a jigsaw puzzle. If this were impossible, that would mean an aperiodic tiling could be made with a set of Wang dominoes. At the time, Wang thought the problem was solvable (therefore no set of aperiodic Wang dominoes could exist), but over the years, other mathematicians — including his student — proved him wrong and created simpler and simpler aperiodic sets of Wang dominoes. Finally, in 1971, Raphael Robinson used the same technique to achieve a set of just six aperiodic tiles (pictured below).
This was the most well-known set of aperiodic tiles before Roger Penrose discovered the three types of Penrose tiling.
This paper will explore the different types of periodic tiling, the math behind their unpredictable and non-periodic nature, and the rules that must be followed to create proper periodic tiling.
Next Section: Concepts to Know Before Learning About Penrose Tiling