Contents
[hide]Concepts to Know Before Learning About Penrose Tiling
Tiling
A tiling is formally defined as a covering of a plane utilizing one or more geometric shapes, commonly known as tiles, with no overlaps or gaps. This can also be called a tessellation. There are two types of tiling: periodic tiling and aperiodic tiling.
Periodic Tiling
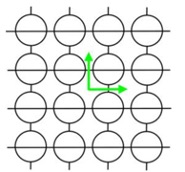
Periodic tiling is tiling in which simple translations of the tiles would result in the same image. For example, if one cuts out a section of the tiling and translates it in any direction, the resulting image will be exactly that of the original image. Below are two examples of periodic tiling (Cornell, 2008).
To better understand this, a basic explanation of translational symmetry should be given.
Translational Symmetry
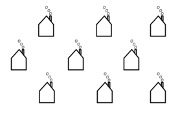
Translational symmetry is a property that an image possesses when it can undergo a movement, such as a shift or a slide, in a specified direction at a specific distance without any rotation or reflection and still produce the same image. Periodic tiling possesses this property of having translational symmetry. An example of translational symmetry is shown below (Study.com).
In this image, if one of the houses is shifted to the left or right at a specific distance, it will produce the same image and continue to produce the same image with further horizontal shifts. If one of the houses is shifted at the specified angle diagonally left or right upwards or downwards, it will also produce the same image. This is the case with periodic tiling, except there are no gaps between the images.
Aperiodic Tiling
Aperiodic tiling is tiling that is only non-periodic, which is the opposite of periodic, meaning that a simple translation of the image could not produce the same image. When tessellations are described as periodic or non-periodic, it can pertain to only a section of the tiling or the entire tiling itself, which is infinite. Aperiodic tiling is a subcategory of non-periodic tiling. Because periodic and non-periodic are terms that can be used to describe a section of tiling, it is possible for a tiling to be periodic at certain parts and non-periodic at others. To reiterate, aperiodic tiling contains only non-periodic tiling. This is a unique characteristic of Penrose tiling.
Penrose Tiling
Penrose tiling is a unique subcategory of aperiodic tiling. It is named after the mathematician and physicist Roger Penrose, who discovered and looked into this type of tiling in the 1970s. Although Penrose tiling is aperiodic, thus not having any translational symmetry, it can possess reflection symmetry and fivefold rotational symmetry.
Reflection Symmetry
Reflection symmetry is a characteristic that an image possesses when one half of the image is the reflection of the other half. In other words, if the image was flipped across the axis of symmetry, the image would result in the pre-image. This is also known as line symmetry or mirror symmetry.
Fivefold Rotational Symmetry
Fivefold rotational symmetry is a characteristic that an image possesses when the image can be rotated five times to achieve the same image until returning to the original position. The most common example of fivefold rotational symmetry is a pentagon. To determine the rotation angle of an object, first determine what fold rotational symmetry it has. If an image has n-fold rotational symmetry, then the rotation angle is 2π/n, since a circle has an angle of 2π. This is then divided by n because that is how many times the image can be rotated to achieve the same image until returning to the original position. Thus for fivefold rotational symmetry, the rotation angle is 2π/5. This means that when a pentagon is rotated at angle of 2π/5, it will result in the original image and can be rotated another four times to return to the original position. This is also a unique characteristic of Penrose tiling.
More Facts!
There are still a few more things to address before discussing the types of Penrose tiling. The original form of Penrose tiling used four different shapes, but this later got changed to only having two shapes, which can be simply seen as two categories. The first category is rhombi. This can then be broken down into two different types of rhombi, which will be further discussed in the Third Penrose Tiling/Rhombus Tiling (P3) section. The second category is quadrilaterals, which can then be split into kites and darts. This will be further discussed in the Second Penrose Tiling/Kite and Dart Tiling (P2) section. Essentially, the four original shapes got split into two broader categories. Two pieces of terminology that should be addressed are period and prototile. A period of tiling is a shift that preserves the tiling in the same way. This is similar to a period of a trigonometric function. A prototile is one of the shapes of a tile in a tessellation. In the following section, the First Penrose Tiling/Original Pentagonal Tiling (P1) will be discussed.
Previous Section: Introduction
Next Section: First Penrose Tiling/Original Pentagonal Tiling (P1)