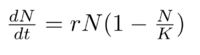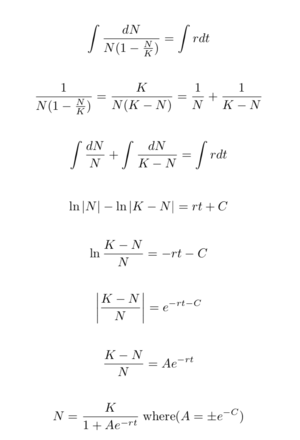m |
|||
| (43 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
==Logistic Models== | ==Logistic Models== | ||
| − | + | ---- | |
==== I. Classic Logistic Models ==== | ==== I. Classic Logistic Models ==== | ||
| − | After realizing limitations of the exponential model, we may wonder: can we do better? We know that the resources are not unlimited. Therefore, at some point, the growth rate must slow down and eventually the population should reach the place where the environment cannot hold more. Based on the above description, it is reasonable to come up | + | After realizing limitations of the exponential model, we may wonder: can we do better? We know that the resources are not unlimited. Therefore, at some point, the growth rate must slow down and eventually the population should reach the place where the environment cannot hold more. Based on the above description, it is reasonable to come up with a graph like this: |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | <center>[[File:5_1.png|300px|left]] | |
| + | <small>''Figure 1 An explanation of logistic growth model Adapted from Lumen Boundless Biology 2013''</small><small></small></center> | ||
| + | |||
| + | Mathematically, we have a model, which is called the Logistic Equation. | ||
| + | |||
| + | <center>[[File:5_12.png|300px|left]] | ||
| + | |||
| + | <small>''Figure 2 An explanation about the growth rate changes over time Adapted from Lumen Boundless Biology''</small> <small></small></center> | ||
| − | |||
For the moment, let’s just ignore the equation f(x) on the right. We’ll cover the mathematical part in the later section. Right now, we’re focusing on the actual meaning of this graph. Let’s check together whether this graph has all the features we discussed before. | For the moment, let’s just ignore the equation f(x) on the right. We’ll cover the mathematical part in the later section. Right now, we’re focusing on the actual meaning of this graph. Let’s check together whether this graph has all the features we discussed before. | ||
| − | By taking the tangent line of each pair of points along the x-axles, we find that the slope is indeed getting smaller and smaller. And when x is sufficiently large, the slope is close to 0. It means, the growth rate of population decreases in each period of years. And after a long time, the number of populations becomes stable. It makes sense intuitively. Please be aware that the decline | + | By taking the tangent line of each pair of points along the x-axles, we find that the slope is indeed getting smaller and smaller. And when x is sufficiently large, the slope is close to 0. It means, the growth rate of the population decreases in each period of years. And after a long time, the number of populations becomes stable. It makes sense intuitively. Please be aware that the decline in growth rate does not indicate the drop of the population. On the contrary, the total population is still increasing as shown in the graph. For more advanced readers, the growth rate is represented by the derivative of the function. And the carrying capacity is the limit of the function when x approaches infinity. |
The actual formula was first proposed by the Belgium mathematician Pierre-François Verhulst in 1835, who stated “The virtual increase of population is limited by the size and the fertility of the country. As a result, the population gets closer and closer to a steady state” in his Note on the law of population growth. (1838 as cited in Bacaër, 2011,) | The actual formula was first proposed by the Belgium mathematician Pierre-François Verhulst in 1835, who stated “The virtual increase of population is limited by the size and the fertility of the country. As a result, the population gets closer and closer to a steady state” in his Note on the law of population growth. (1838 as cited in Bacaër, 2011,) | ||
| + | <center>[[File:5_14.png|200px|left]]</center> | ||
| − | Here N, K, r represent population, carrying capacity, and a growth rate parameter respectively. Noted the formula is given in the differentiation form. | + | Here N, K, r represent the population, carrying capacity, and a growth rate parameter respectively. Noted the formula is given in the differentiation form. |
This model assumes that the growth rate r is linear and it is decreasing in terms of N. In other words, r_a=F(N). For a more complete model, we will introduce r_m as the max growth rate. But it is beyond our text slope. | This model assumes that the growth rate r is linear and it is decreasing in terms of N. In other words, r_a=F(N). For a more complete model, we will introduce r_m as the max growth rate. But it is beyond our text slope. | ||
| − | Interestingly, if N(t) is much smaller than K, this ordinary equation is | + | Interestingly, if N(t) is much smaller than K, this ordinary equation is approximate as |
our previous exponential model. Here comes another question. Can we write N(t) explicitly just like the exponential one? | our previous exponential model. Here comes another question. Can we write N(t) explicitly just like the exponential one? | ||
| − | The exciting answer is yes! But understanding how to get it requires some math background in an introductory level ordinary differential equation class. We strongly encourage interested readers take MA366 or MA 266 held by Purdue math department. | + | The exciting answer is yes! But understanding how to get it requires some math background in an introductory level ordinary differential equation class. We strongly encourage interested readers to take MA366 or MA 266 held by Purdue math department. |
Let’s do some math! | Let’s do some math! | ||
| + | <center>[[File:5_13.png|300px|left]] | ||
| + | <small>''Figure 3 Merma, 2004 P80 The logistic equation Adapted from Northwestern University website''</small><small></small></center> | ||
| + | And we ’ll see in a later section that even the complicated logistic equation cannot predict the population accurately. | ||
| + | ==== II.Theta Logistic model ==== | ||
| + | Even though the logistic model includes more population growth factors, the basic logistic model is still not good enough. | ||
| − | + | In order to fit data better and address the limitations from the classic logistic model, Gilpin and Ayala(1973) presented a new version of the logistic model (as cited in Clark et al., 2010) called “theta-logistic model”. | |
| − | + | As a large population size continues to grow, the individual growth rate should slow down. This new finding is not included in the classical model. The new theta-logistic model, however, takes this into account. (Clark et al., 2010) | |
| + | A new term θ is added to the classic logistic model. The linear density dependence held by the | ||
| + | classical logistic model can be altered to curvilinear. It is this θ that provides the additional generality and flexibility to explain the impact by the change of individual growth rate parameter r_a with respect to population density N. (Salisbury,2011) | ||
| + | How does θ work mathematically in this model? With the variation of θ, it can reflect the relation between infraspecific competition and population density. In the classic logistic model, we have[[File:Graph_5.5.png|100px]]instead, where r_m is the maximum growth rate which decreases linearly as N increases. | ||
| − | + | Now in the new theta-logistic model, we have [[File:Graph_5.2.2.png|100px]] instead. Notice that with θ=1, it becomes the basic logistic model; with θ=0, we have zero-growth model. | |
| − | + | What happens when θ takes other values then? | |
| − | + | The following graph demonstrates four different cases with θ>1 or θ<1. | |
| − | + | <center>[[File:Graph_5.2.3.png|300px]] </center> | |
| − | + | <center> <small>''Figure 4: Four different cases with θ>1 or θ<1]]''</small><small></small></center> | |
| − | + | ||
| − | + | This graph shows a typical pattern of how various values of θ change the shape of the growth response curve with r_m=0.5 and K=100. As θ>1, when r>0, the growth response curve is concave down while as θ<1, the growth response curve is concave up. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | And now we are ready to derive the new model! | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | After substituting our updated growth rate r_a into our original logistic equation, we obtain the theta-logistic growth model: | |
| − | + | <center>[[File:Graph_5.2.4.png|200px]]</center> | |
| − | < | + | |
| − | File:Graph_5.2. | + | |
| − | </ | + | |
| − | + | Notice that | |
| − | + | <center>[[File:Graph_5.2.5.png|200px]]</center> | |
| − | + | That is: when we set θ>1, the carrying capacity term has more weight(compares to the previous model because the first term of the formula is smaller now). Thus it weakens the density-dependence for low values of N. And when we set θ<1, the density dependence is strengthened for low values of N, leading to slower population growth. These two different scenarios could be summarized in the following graph: | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | < | + | |
| − | + | <center>[[File:Graph_5.2.6.png|300px]]</center> | |
| − | < | + | |
| − | File: | + | |
| − | + | ||
| − | </ | + | |
| − | + | <center><small>''Figure 5: Phase line portrait of theta-logistic model, described by Eq. (2.28), for arbitrary values of θ = (0.5, 1, 3, 10)''</small><small></small></center> | |
| − | < | + | |
| − | + | ||
| − | + | ||
| − | </ | + | |
| − | + | Does the model perfectly fit our census data of population? | |
| − | + | ||
| − | + | ||
Unfortunately, the answer is still no. | Unfortunately, the answer is still no. | ||
| − | In | + | In a research paper published in 2010, Francis et al. (2010) demonstrated that when they were fitting a theta-logistic model with the most census data, it was not robust! With the time series they used, r was not a reliable estimation of the growth response rate. They concluded that more ecological clarification on the concept of carrying capacity is needed in order to develop further research study. |
==== III.Logistic Model with Allee’s Effect ==== | ==== III.Logistic Model with Allee’s Effect ==== | ||
| − | We talked about how the population grows and how carrying capacity works | + | We already talked about how the population grows and how the carrying capacity works. But we have not seen what would happen if there is only a small population. The classical view of population dynamics expressed that the growth rate of a population will decrease at higher density and increase at lower density due to competition for limited resources. However, the Allee effect (derived from Warder Clyde Allee’s “Allee principle” introduced in the 1950s) describes a situation where when the density is low, the population growth rate also decreases because of “limited mate availability and impaired cooperative behaviors”,according to Alexander Salisbury’s Mathematical Models in Population Dynamics,(2011, p.61). The following graph clearly shows the difference between the classical dynamics and Allee effect which has a positive density dependence, the positive correlation between population density and individual fitness (often measured as per capita population growth rate). |
| − | [[Image:Figure531.jpg]] | + | <center>[[Image:Figure531.jpg]]</center> |
| − | Adapted from Courchamp, Ludek, &Gascoigne, 2008. | + | <center><small>Figure 6: Adapted from Courchamp, Ludek, &Gascoigne, 2008.</small><small></small></center> |
| − | According to Alexander, to begin incorporating the Allee effect into a normal logistic growth, we need to find the Allee threshold, above which the population will continue by ordinary logistic growth, and below which the population will decay (due to Allee effect) (2011). A simple mathematical example of an Allee effect from wikipedia (Salisbury, 2011, 62) is given by the cubic growth model, <math>\frac{dN}{dT}=rN(\frac{N}{T}-1)(1-\frac{N}{K})</math> where | + | According to Alexander, to begin incorporating the Allee effect into a normal logistic growth, we need to find the Allee threshold, above which the population will continue by ordinary logistic growth, and below which the population will decay (due to Allee effect) (2011). A simple mathematical example of an Allee effect from wikipedia (Salisbury, 2011, p.62) is given by the cubic growth model, <math>\frac{dN}{dT}=rN(\frac{N}{T}-1)(1-\frac{N}{K})</math> where |
N = population size; | N = population size; | ||
r = intrinsic rate of increase; | r = intrinsic rate of increase; | ||
| Line 121: | Line 102: | ||
<math>\frac{dN}{dT}</math> = rate of increase of the population. | <math>\frac{dN}{dT}</math> = rate of increase of the population. | ||
| − | [[Image:Figure532.jpg]] | + | <center>[[Image:Figure532.jpg]]</center> |
| + | |||
| + | <center><small>Figure 7: Dynamics of the Allee effect. Adapted from “Mathematical Models in Population Dynamics,” by Alexander Salisbury, 2011. </small><small></small></center> | ||
| + | |||
| + | This graph is an example of a strong Allee effect where the population has a negative growth rate for 0 < N < T and are eventually driven to extinction, and a positive growth rate for T < N < K (assuming 0 < T < K). In cases of a weak Allee effect, populations below the threshold are merely hampered in their rates of growth. The occurrences of Allee effect are more easily observed from small populations as populations above the threshold follow a logistic growth. Since human population has never dropped to such a low level, there is no research concerning about influence of Allee effect to the human population, but Allee effect has been observed in many species, especially animals that hunt for prey or defend against predators as a group. | ||
| − | |||
| − | |||
| − | + | [[Failure_of_the_models|Next Section: Failure of the models]] | |
| + | [[Before_logistic_model|Previous Section: Before logistic model]] | ||
| − | [[ Walther MA279 Fall2018 topic10|Back to Walther MA279 Fall2018 | + | [[ Walther MA279 Fall2018 topic10|Back to Walther MA279 Fall2018 Topic10 Home Page]] |
Latest revision as of 21:51, 2 December 2018
Contents
Logistic Models
I. Classic Logistic Models
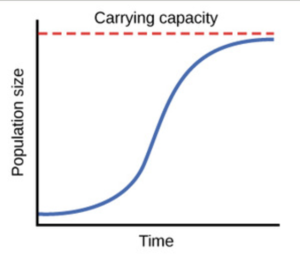
After realizing limitations of the exponential model, we may wonder: can we do better? We know that the resources are not unlimited. Therefore, at some point, the growth rate must slow down and eventually the population should reach the place where the environment cannot hold more. Based on the above description, it is reasonable to come up with a graph like this:
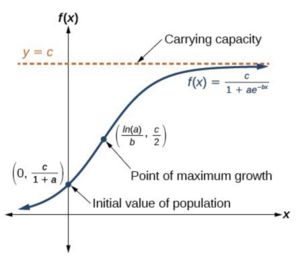
Mathematically, we have a model, which is called the Logistic Equation.
For the moment, let’s just ignore the equation f(x) on the right. We’ll cover the mathematical part in the later section. Right now, we’re focusing on the actual meaning of this graph. Let’s check together whether this graph has all the features we discussed before.
By taking the tangent line of each pair of points along the x-axles, we find that the slope is indeed getting smaller and smaller. And when x is sufficiently large, the slope is close to 0. It means, the growth rate of the population decreases in each period of years. And after a long time, the number of populations becomes stable. It makes sense intuitively. Please be aware that the decline in growth rate does not indicate the drop of the population. On the contrary, the total population is still increasing as shown in the graph. For more advanced readers, the growth rate is represented by the derivative of the function. And the carrying capacity is the limit of the function when x approaches infinity.
The actual formula was first proposed by the Belgium mathematician Pierre-François Verhulst in 1835, who stated “The virtual increase of population is limited by the size and the fertility of the country. As a result, the population gets closer and closer to a steady state” in his Note on the law of population growth. (1838 as cited in Bacaër, 2011,)
Here N, K, r represent the population, carrying capacity, and a growth rate parameter respectively. Noted the formula is given in the differentiation form. This model assumes that the growth rate r is linear and it is decreasing in terms of N. In other words, r_a=F(N). For a more complete model, we will introduce r_m as the max growth rate. But it is beyond our text slope.
Interestingly, if N(t) is much smaller than K, this ordinary equation is approximate as our previous exponential model. Here comes another question. Can we write N(t) explicitly just like the exponential one?
The exciting answer is yes! But understanding how to get it requires some math background in an introductory level ordinary differential equation class. We strongly encourage interested readers to take MA366 or MA 266 held by Purdue math department.
Let’s do some math!
And we ’ll see in a later section that even the complicated logistic equation cannot predict the population accurately.
II.Theta Logistic model
Even though the logistic model includes more population growth factors, the basic logistic model is still not good enough.
In order to fit data better and address the limitations from the classic logistic model, Gilpin and Ayala(1973) presented a new version of the logistic model (as cited in Clark et al., 2010) called “theta-logistic model”.
As a large population size continues to grow, the individual growth rate should slow down. This new finding is not included in the classical model. The new theta-logistic model, however, takes this into account. (Clark et al., 2010)
A new term θ is added to the classic logistic model. The linear density dependence held by the classical logistic model can be altered to curvilinear. It is this θ that provides the additional generality and flexibility to explain the impact by the change of individual growth rate parameter r_a with respect to population density N. (Salisbury,2011)
How does θ work mathematically in this model? With the variation of θ, it can reflect the relation between infraspecific competition and population density. In the classic logistic model, we have![]() instead, where r_m is the maximum growth rate which decreases linearly as N increases.
instead, where r_m is the maximum growth rate which decreases linearly as N increases.
Now in the new theta-logistic model, we have 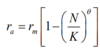 instead. Notice that with θ=1, it becomes the basic logistic model; with θ=0, we have zero-growth model.
instead. Notice that with θ=1, it becomes the basic logistic model; with θ=0, we have zero-growth model.
What happens when θ takes other values then?
The following graph demonstrates four different cases with θ>1 or θ<1.
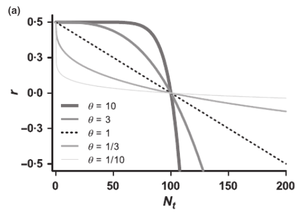
This graph shows a typical pattern of how various values of θ change the shape of the growth response curve with r_m=0.5 and K=100. As θ>1, when r>0, the growth response curve is concave down while as θ<1, the growth response curve is concave up.
And now we are ready to derive the new model!
After substituting our updated growth rate r_a into our original logistic equation, we obtain the theta-logistic growth model:
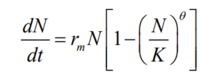
Notice that
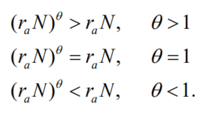
That is: when we set θ>1, the carrying capacity term has more weight(compares to the previous model because the first term of the formula is smaller now). Thus it weakens the density-dependence for low values of N. And when we set θ<1, the density dependence is strengthened for low values of N, leading to slower population growth. These two different scenarios could be summarized in the following graph:
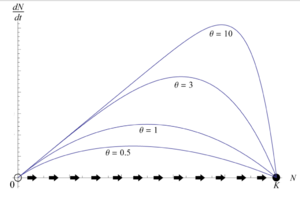
Does the model perfectly fit our census data of population? Unfortunately, the answer is still no.
In a research paper published in 2010, Francis et al. (2010) demonstrated that when they were fitting a theta-logistic model with the most census data, it was not robust! With the time series they used, r was not a reliable estimation of the growth response rate. They concluded that more ecological clarification on the concept of carrying capacity is needed in order to develop further research study.
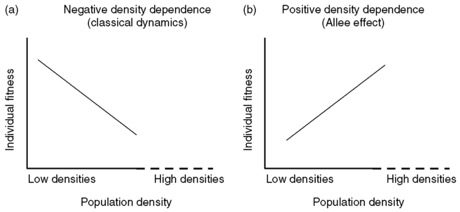
III.Logistic Model with Allee’s Effect
We already talked about how the population grows and how the carrying capacity works. But we have not seen what would happen if there is only a small population. The classical view of population dynamics expressed that the growth rate of a population will decrease at higher density and increase at lower density due to competition for limited resources. However, the Allee effect (derived from Warder Clyde Allee’s “Allee principle” introduced in the 1950s) describes a situation where when the density is low, the population growth rate also decreases because of “limited mate availability and impaired cooperative behaviors”,according to Alexander Salisbury’s Mathematical Models in Population Dynamics,(2011, p.61). The following graph clearly shows the difference between the classical dynamics and Allee effect which has a positive density dependence, the positive correlation between population density and individual fitness (often measured as per capita population growth rate).
According to Alexander, to begin incorporating the Allee effect into a normal logistic growth, we need to find the Allee threshold, above which the population will continue by ordinary logistic growth, and below which the population will decay (due to Allee effect) (2011). A simple mathematical example of an Allee effect from wikipedia (Salisbury, 2011, p.62) is given by the cubic growth model, $ \frac{dN}{dT}=rN(\frac{N}{T}-1)(1-\frac{N}{K}) $ where N = population size; r = intrinsic rate of increase; K = carrying capacity; T = Allee threshold; $ \frac{dN}{dT} $ = rate of increase of the population.
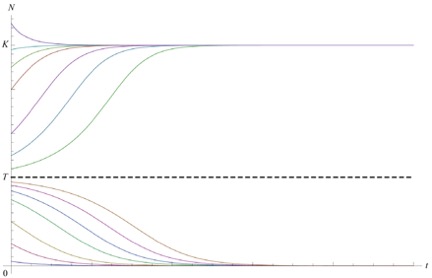
This graph is an example of a strong Allee effect where the population has a negative growth rate for 0 < N < T and are eventually driven to extinction, and a positive growth rate for T < N < K (assuming 0 < T < K). In cases of a weak Allee effect, populations below the threshold are merely hampered in their rates of growth. The occurrences of Allee effect are more easily observed from small populations as populations above the threshold follow a logistic growth. Since human population has never dropped to such a low level, there is no research concerning about influence of Allee effect to the human population, but Allee effect has been observed in many species, especially animals that hunt for prey or defend against predators as a group.
Next Section: Failure of the models