Revision as of 21:03, 1 May 2017

ECE Ph.D. Qualifying Exam in Communication Networks Signal and Image processing (CS)

Question 5, August 2013(Published on May 2017),

Problem 1,2

Solution 1:

a) If the color matching functions f_k(λ) has negative values, it will result in negative values in F_k. In this case, the color can not be reproduced by this device.

b) The CIE color matching functions are not always positive. This is the case because, to match some reference color that is too saturated, colors have to be subtracted from the R,G, and B primaries. This results in negative values in tristimulus values r, g, and b. So the color matching functions at the corresponding wavelength have negative values.

c)
$ \left[ {\begin{array}{*{20}{c}} F_1\\ F_2\\ F_3 \end{array}} \right] = {\begin{array}{*{20}{c}} \int_{-\infty}^{\infty} \end{array}} \left[ {\begin{array}{*{20}{c}} f_1(\lambda)\\ f_1(\lambda)\\ f_1(\lambda) \end{array}} \right] I(\lambda)d\lambda = {\begin{array}{*{20}{c}} \int_{-\infty}^{\infty} \end{array}} M \left[ {\begin{array}{*{20}{c}} r_0(\lambda)\\ g_0(\lambda)\\ b_0(\lambda) \end{array}} \right] I(\lambda)d\lambda = M {\begin{array}{*{20}{c}} \int_{-\infty}^{\infty} \end{array}} \left[ {\begin{array}{*{20}{c}} r_0(\lambda)\\ g_0(\lambda)\\ b_0(\lambda) \end{array}} \right] I(\lambda)d\lambda = M \left[ {\begin{array}{*{20}{c}} r\\ g\\ b \end{array}} \right] $

So that, [r,g,b]^t = M ^{− 1}[F₁,F₂,F₃].

missed transpose sign on F. It should be [r,g,b]^t = M ^{− 1}[F₁,F₂,F₃]^t.

d) It exists. CIE XYZ is one example. However, XYZ has problems with its primaries, since, the primary colors are imaginary.

Solution 2:

a) f₁(λ), f₂(λ) and f₃(λ) are the spectral functions for the three color outputs of color camera. It must be positive because we cannot produce negative spectrum. 

b) No. r_o(λ),g_o(λ)a'n'd'b_o(λ) are CIE color matching. It takes negative value in order to substract some color to be saturated. 

c)

 $ \left[ {\begin{array}{*{20}{c}} F_1\\ F_2\\ F_3 \end{array}} \right] = {\begin{array}{*{20}{c}} \int_{-\infty}^{\infty} \end{array}} \left[ {\begin{array}{*{20}{c}} f_1(\lambda)\\ f_2(\lambda)\\ f_3(\lambda) \end{array}} \right] I(\lambda)d\lambda = {\begin{array}{*{20}{c}} \int_{-\infty}^{\infty} \end{array}} M \left[ {\begin{array}{*{20}{c}} r_0(\lambda)\\ g_0(\lambda)\\ b_0(\lambda) \end{array}} \right] I(\lambda)d\lambda = M {\begin{array}{*{20}{c}} \int_{-\infty}^{\infty} \end{array}} \left[ {\begin{array}{*{20}{c}} r_0(\lambda)\\ g_0(\lambda)\\ b_0(\lambda) \end{array}} \right] I(\lambda)d\lambda = M \left[ {\begin{array}{*{20}{c}} r\\ g\\ b \end{array}} \right] $

d)

Yes. They exist. If there is a matrix M that exist to satisfy this equation  $ \left[ {\begin{array}{*{20}{c}} f_1(\lambda)\\ f_2(\lambda)\\ f_3(\lambda) \end{array}} \right] = M \left[ {\begin{array}{*{20}{c}} r_0(\lambda)\\ g_0(\lambda)\\ b_0(\lambda) \end{array}} \right] $. 

The student can be more specific on the example of such case. I am not sure what is a good example either. Will consult Professor to figure it out.

Related Problem

1. In a color matching experiment, the three primaries R, G, B are used to match the color of a pure spectral component at wavelength λ. Here the color matching allows for color to be subtracted from the reference color. At each wavelength λ, the matching color is given by

$ \left[ {\begin{array}{*{20}{c}} R, G, B \end{array}} \right] \left[ {\begin{array}{*{20}{c}} r(\lambda)\\ g(\lambda)\\ b(\lambda) \end{array}} \right] $

where r₍λ), g₍λ), and b₍λ) are normalized to 1.

Further define the white point

$ W = \left[ {\begin{array}{*{20}{c}} R, G, B \end{array}} \right] \left[ {\begin{array}{*{20}{c}} r_w\\ g_w\\ b_w \end{array}} \right] $

Let I(λ) be the light reflected from a surface.

a) Calculate (r_e,g_e,b_e) the tristimulus values for the spectral distribution I(λ) using primaries R,G,B and an equal energy white point.

b) Calculate (r_c,g_c,b_c) the tristimulus values for the spectral distribution I(λ) using primaries R,G,B and white point (r_w,g_w,b_w).

(Refer to ECE637 2004 Final Problem 4.)

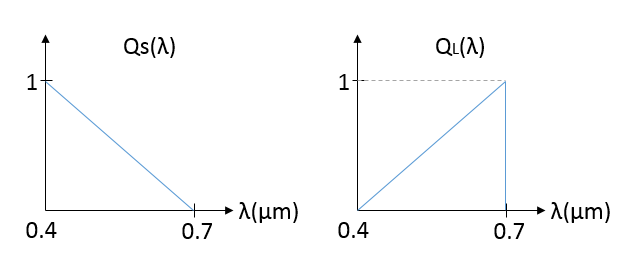
2. Consider the two channel sensors with response function Q_S(λ) and Q_L(λ). Suppose that we have two primaries P_L(λ) = σ(λ − 0.6) and P_S(λ) = σ(λ − 0.5).

Find the color matching function $ \bar{l}(\lambda) $ and $ \bar{s}(\lambda) $ for these two primaries.

(Refer to ECE638 Lecture note 3: Trichromatic theory of color.)

Back to ECE QE page: