| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | [[Category: | + | [[Category:HW4ECE438F14]] |
| − | =Homework 4, [[ECE438 | + | =[[HW4ECE438F14|Homework 4]] Solution, [[2014_Fall_ECE_438_Boutin| ECE438 Fall 2014]], [[user:mboutin|Prof. Boutin]]= |
---- | ---- | ||
| Line 29: | Line 29: | ||
The sampling rate <math>f_s=12</math>samples/year. The periodic component has frequency of <math>f_c=1</math>cycle/year. | The sampling rate <math>f_s=12</math>samples/year. The periodic component has frequency of <math>f_c=1</math>cycle/year. | ||
| − | The cutoff frequency | + | The cutoff frequency of the ideal LPF is |
<math>\omega_c=\frac{2\pi \cdot 1}{12}=\frac{\pi}{6}</math> | <math>\omega_c=\frac{2\pi \cdot 1}{12}=\frac{\pi}{6}</math> | ||
| Line 44: | Line 44: | ||
Y(w) &= \sum_{n=-\infty}^{\infty} y[n]e^{-jwn} = \sum_{n=-\infty}^{\infty} x[Dn]e^{-jwn} \\ | Y(w) &= \sum_{n=-\infty}^{\infty} y[n]e^{-jwn} = \sum_{n=-\infty}^{\infty} x[Dn]e^{-jwn} \\ | ||
&= \sum_{m=-\infty, m=Dk}^{\infty} x[m]e^{-j\frac{wm}{D}} = \sum_{m=-\infty}^{\infty} x[m] \left( \sum_{k=-\infty}^{\infty} \delta[m-Dk] \right) e^{-j\frac{wm}{D}} \\ | &= \sum_{m=-\infty, m=Dk}^{\infty} x[m]e^{-j\frac{wm}{D}} = \sum_{m=-\infty}^{\infty} x[m] \left( \sum_{k=-\infty}^{\infty} \delta[m-Dk] \right) e^{-j\frac{wm}{D}} \\ | ||
| − | &= \sum_{m=-\infty}^{\infty} x[m] \left( \frac{1}{D} \sum_{k=0}^{D-1} e^{j\frac{2\pi}{D}km} \right) e^{-j\frac{wm}{D}} = \sum_{k=0}^{D-1} \frac{1}{D} \sum_{m=-\infty}^{\infty} x[m]e^{j\left(w-\frac{2\pi}{D}k\right)m} \\ | + | &= \sum_{m=-\infty}^{\infty} x[m] \left( \frac{1}{D} \sum_{k=0}^{D-1} e^{j\frac{2\pi}{D}km} \right) e^{-j\frac{wm}{D}} = \sum_{k=0}^{D-1} \frac{1}{D} \sum_{m=-\infty}^{\infty} x[m]e^{j\left(\frac{w}{D}-\frac{2\pi}{D}k\right)m} \\ |
&= \sum_{k=0}^{D-1} \frac{1}{D} X\left(\frac{w-2\pi k}{D}\right) \\ | &= \sum_{k=0}^{D-1} \frac{1}{D} X\left(\frac{w-2\pi k}{D}\right) \\ | ||
\end{align}</math> | \end{align}</math> | ||
| Line 72: | Line 72: | ||
a) Under what circumstances is the downsampling xD[n] = x1[Dn] equivalent to a resampling of the signal with a new period equal to DT (i.e. xD[n] = x(DTn))? | a) Under what circumstances is the downsampling xD[n] = x1[Dn] equivalent to a resampling of the signal with a new period equal to DT (i.e. xD[n] = x(DTn))? | ||
| − | + | '''Solution''' | |
| − | <math> | + | <math>x_D[n]=x_1[Dn]=x(DnT)</math> |
| − | + | ||
| − | + | ||
| − | + | This is true for any integer D. | |
| − | + | b) Under what circumstances is it possible to construct the sampling <math>x_3[n]= x(\frac{T}{D} n) </math> directly from <math>x_1[n]</math> (without reconstructing x(t))? | |
| − | + | '''Solution''' | |
| + | It is always possible. | ||
---- | ---- | ||
Latest revision as of 05:24, 10 October 2014
Contents
Homework 4 Solution, ECE438 Fall 2014, Prof. Boutin
Question 1
Conversion between analog and digital frequencies
To prevent aliasing, the sampling rate should be higher or equal to twice of the highest frequency of the signal.
$ \begin{align} f_s=2 \cdot 2500=5000Hz \end{align} $
So the sampling frequency should be greater than 5000Hz.
We need a high pass filter that filters out signals below the frequency 60Hz.
$ \begin{align} \omega_c=\frac{2\pi \cdot f_c }{f_s}=\frac{2\pi \cdot 60 }{5000} \end{align} $
Question 2
Conversion between analog and digital frequencies
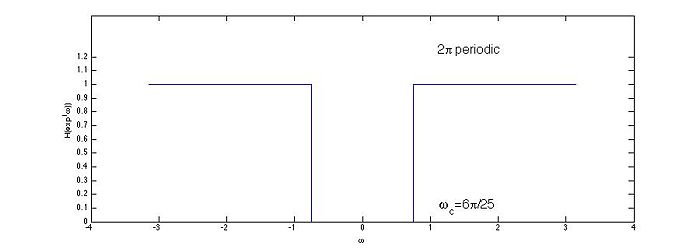
We can think of the long term trend as low frequency component and annual cycle as high frequency component. In order to remove the annual cycle, we need a low pass filter. The sampling rate $ f_s=12 $samples/year. The periodic component has frequency of $ f_c=1 $cycle/year.
The cutoff frequency of the ideal LPF is
$ \omega_c=\frac{2\pi \cdot 1}{12}=\frac{\pi}{6} $
Question 3
Downsampling and upsampling
$ \text{a)} \;\; \text{General Relation for the decimation with a factor of } D \,\! $.
$ \text{Let } X(w) = \mathcal{F}(x[n]) $
$ \begin{align} Y(w) &= \sum_{n=-\infty}^{\infty} y[n]e^{-jwn} = \sum_{n=-\infty}^{\infty} x[Dn]e^{-jwn} \\ &= \sum_{m=-\infty, m=Dk}^{\infty} x[m]e^{-j\frac{wm}{D}} = \sum_{m=-\infty}^{\infty} x[m] \left( \sum_{k=-\infty}^{\infty} \delta[m-Dk] \right) e^{-j\frac{wm}{D}} \\ &= \sum_{m=-\infty}^{\infty} x[m] \left( \frac{1}{D} \sum_{k=0}^{D-1} e^{j\frac{2\pi}{D}km} \right) e^{-j\frac{wm}{D}} = \sum_{k=0}^{D-1} \frac{1}{D} \sum_{m=-\infty}^{\infty} x[m]e^{j\left(\frac{w}{D}-\frac{2\pi}{D}k\right)m} \\ &= \sum_{k=0}^{D-1} \frac{1}{D} X\left(\frac{w-2\pi k}{D}\right) \\ \end{align} $
Replacing D with 4 would be the answer.
$ \text{b)} \;\; \text{General Relation for the upsampling with a factor of } L \,\! $.
$ \begin{align} Z(w) &= \sum_{n=-\infty}^{\infty} z[n]e^{-jwn} \\ &= \sum_{n=-\infty}^{\infty} \left( \sum_{k=-\infty}^{\infty} x[k] \delta[n-kL] \right) e^{-jwn} \\ &= \sum_{k=-\infty}^{\infty} x[k] \sum_{n=-\infty}^{\infty} \delta[n-kL] e^{-jwn} = \sum_{k=-\infty}^{\infty} x[k] e^{-jwkL} \\ &= \sum_{k=-\infty}^{\infty} x[k] e^{-jLwk} = X(Lw) \\ &\end{align} $
Since $ X(w) $ is periodic with $ 2\pi $, $ Z(w)=X(Lw) $ is periodic with $ 2\pi/L $.
Replaing L with 4 would be the answer.
Question 4
Downsampling and upsampling
Let x1[n] = x(Tn) be a sampling of a CT signal x(t). Let D be a positive integer.
a) Under what circumstances is the downsampling xD[n] = x1[Dn] equivalent to a resampling of the signal with a new period equal to DT (i.e. xD[n] = x(DTn))?
Solution
$ x_D[n]=x_1[Dn]=x(DnT) $
This is true for any integer D.
b) Under what circumstances is it possible to construct the sampling $ x_3[n]= x(\frac{T}{D} n) $ directly from $ x_1[n] $ (without reconstructing x(t))?
Solution
It is always possible.