| Line 12: | Line 12: | ||
:a. Find the difference equation of this filter. | :a. Find the difference equation of this filter. | ||
| − | :b. Find the frequency response <math>H(w)</math> by the following two approaches: | + | :b. Find the frequency response <math>H(w)</math> from the difference equation by the following two approaches: |
::i. apply the input <math>e^{jwn}</math> to the difference equation describing the system, | ::i. apply the input <math>e^{jwn}</math> to the difference equation describing the system, | ||
::ii. find the DTFT of the impulse response, | ::ii. find the DTFT of the impulse response, | ||
Revision as of 10:25, 19 October 2010
Quiz Questions Pool for Week 9
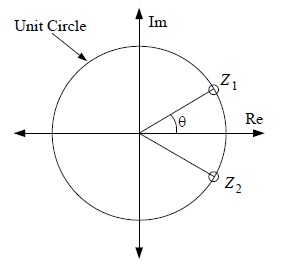
Q1. Consider the following second order FIR filter with the two zeros on the unit circle as shown below.
The transfer function for this filter is given by $ H(z) = (1-e^{j\theta}z^{-1})(1-e^{-j\theta}z^{-1})=1-2\cos\theta z^{-1}+z^{-2} $
- a. Find the difference equation of this filter.
- b. Find the frequency response $ H(w) $ from the difference equation by the following two approaches:
- i. apply the input $ e^{jwn} $ to the difference equation describing the system,
- ii. find the DTFT of the impulse response,
- and verify that both methods lead to the same result.
- c. Find the response of this system to the input
- $ x[n]=\left\{ \begin{array}{rl} 1, & \text{ if }n=-2,\\ 1, & \text{ if }n=0,\\ 1, & \text{ if }n=2,\\ 0, & \text{ else. } \end{array} \right. $
- d. Is this filter a lowpass, highpass, bandpass or a bandstop filter?
- e. An interference signal modulated at 2kHz and sampled at 8kHz is being inputted to this system and you want to eliminate this interference. What must be the value of $ \theta $ to eliminate this signal?
Q2.
Q3.
Q4.
Q5.
Back to ECE 438 Fall 2010 Lab Wiki Page
Back to ECE 438 Fall 2010