| Line 1: | Line 1: | ||
[[Category:2010 Fall ECE 438 Boutin]] | [[Category:2010 Fall ECE 438 Boutin]] | ||
| − | |||
| − | |||
---- | ---- | ||
| Line 71: | Line 69: | ||
* [[ECE438_Week8_Quiz_Q4sol|Solution]]. | * [[ECE438_Week8_Quiz_Q4sol|Solution]]. | ||
| − | |||
| − | |||
| − | |||
---- | ---- | ||
Revision as of 19:25, 12 October 2010
Quiz Questions Pool for Week 8
Q1. Find the impulse response of the following LTI systems and draw their block diagram.
(assume that the impulse response is causal and zero when $ n<0 $)
$ {\color{White}ab}\text{a)}{\color{White}abc}y[n] = 0.6 y[n-1] + 0.4 x[n] $
$ {\color{White}ab}\text{b)}{\color{White}abc}y[n] = y[n-1] + 0.25(x[n] - x[n-3]) $
Q2. Suppose that the LTI filter $ h_1 $ satifies the following difference equation between input $ x[n] $ and output $ y[n] $.
$ {\color{White}ab} y[n] = h_1[n]\;\ast\;x[n] = \frac{1}{4} y[n-1] + x[n] $
($ \ast $ implies the convolution)
Then, find the inverse LTI filter $ h_2 $ of $ h_1 $, which satisfies the following relationship for any discrete-time signal $ x[n] $,
(assume that the impulse responses are causal and zero when $ n<0 $)
$ {\color{White}ab} x[n] = h_2[n]\;\ast\;h_1[n]\;\ast\;x[n] $
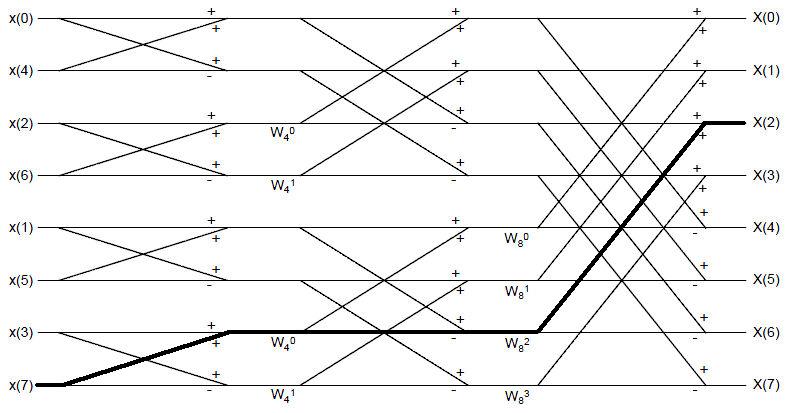
$ \text{Q3.} $
The following figure shows the flow diagram that results for an N=8 FFT algorithm. The bolded line indicates a path from input sample x[7] to DFT sample X[2].
a) What is the gain of the path?
b) How many paths exist beginning at x[7] and ending up at X[2]? Does the result apply to a general condition? i.e. How many paths are there between every input sample and output sample?
c) Consider DFT sample X[2]. Following paths displayed in the flow diagram. Prove that every input sample contributes the proper amount to the output DFT sample.
i.e. $ X[2]=\sum_{n=0}^{N-1} x[n]e^{-j(2\pi /N)2n} $
$ \text{Q4.} $
Consider a system described by the following equation
y[n] = x[n] + x[n-1] + y[n-1]
a. Find the response y[n] to the input
$ x[n] = \begin{cases} (-1)^n, & 0 <= n <= 4 \\ 0, & \mbox{else} \end{cases} $
b. State whether or not this system is (i) linear, (ii) time-invariant, (iii) memoryless, (iv) causal, (v) bounded-input-bounded output stable.
c. Find an expression for the frequency response $ H(\omega) $ for this system.
d. Find the output y[n] when the input x[n] = sin(n$ \pi $/4) using the answer to part c.
e. Find an expression for impulse response h[n].
Back to ECE 438 Fall 2010 Lab Wiki Page
Back to ECE 438 Fall 2010