(→Periodic Functions) |
|||
| Line 1: | Line 1: | ||
| + | = Periodic versus non-periodic function= | ||
| + | As part of the [[Homework_1_ECE301Fall2008mboutin|first homework]] in [[ECE301]] this semester, we were asked to give an example of a periodic function as well as an example of a non-periodic function. Here are my answers. A precise definition of periodic function can be found on my colleague [[HW1.4_Brian_Thomas_-_Periodic_Versus_Non-Periodic_Signals_in_Discrete_Time_ECE301Fall2008mboutin|Brian Thomas' page]]. | ||
| + | |||
== Periodic Functions == | == Periodic Functions == | ||
A periodic function is a function which repeats over a period of time. A good example of periodic functions are: | A periodic function is a function which repeats over a period of time. A good example of periodic functions are: | ||
| Line 14: | Line 17: | ||
:*<math>\,y = e^x</math> | :*<math>\,y = e^x</math> | ||
[[Image:Graph14_ECE301Fall2008mboutin.png]] | [[Image:Graph14_ECE301Fall2008mboutin.png]] | ||
| + | ---- | ||
| + | [[Main_Page_ECE301Fall2008mboutin|Back to ECE301 Fall 2008, Prof. Boutin]] | ||
Revision as of 10:35, 11 March 2010
Periodic versus non-periodic function
As part of the first homework in ECE301 this semester, we were asked to give an example of a periodic function as well as an example of a non-periodic function. Here are my answers. A precise definition of periodic function can be found on my colleague Brian Thomas' page.
Periodic Functions
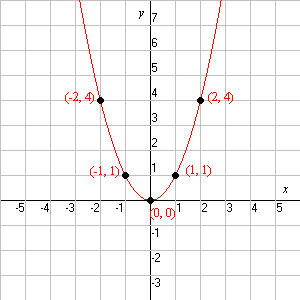
A periodic function is a function which repeats over a period of time. A good example of periodic functions are:
- $ \,y = sin(t) $
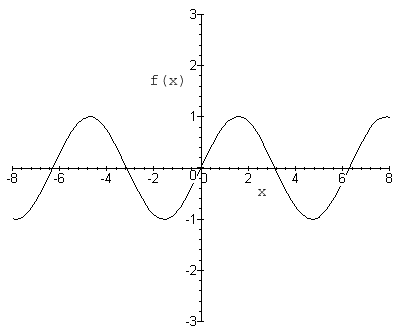As you can see, this function repeats itself with a period of $ 2\pi $
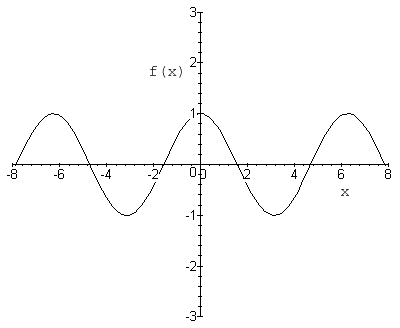
- $ \,y = cos(t) $
As you can see, this function repeats itself with a period of $ 2\pi $
Non-Periodic Functions
Non periodic functions don't repeat. A good example of non-periodic functions are:
- $ \,y = x^2 $
- $ \,y = e^x $
