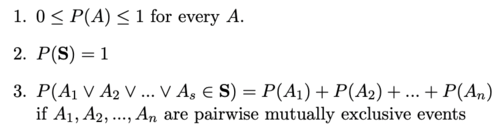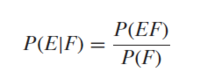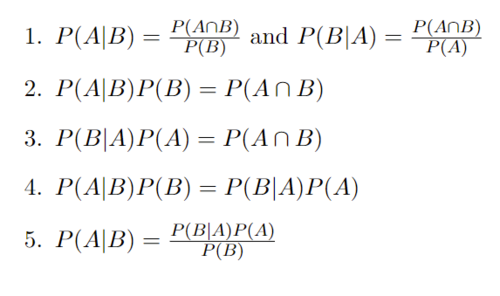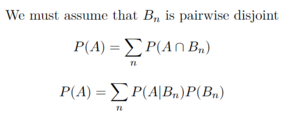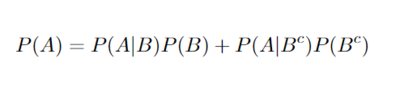Probability : Group 4
Kalpit Patel Rick Jiang Bowen Wang Kyle Arrowood
Probability, Conditional Probability, Bayes Theorem Disease example
Definition: Probability is a measure of the likelihood of an event to occur. Many events cannot be predicted with total certainty. We can predict only the chance of an event to occur i.e., how likely they are going to happen, using it.
Notation:
1) Sample space (S): Set of all possible outcomes of an experiment (e.g., S={O1,O2,..,On}).
2) Event: Any subsets of outcomes (e.g., A={O1,O2,Ok}) contained in the sample space S.
Formula for probability:
1. Let N:= |S| be the size of sample space
2. Let N(A):= |A| be the number of simple outcomes contained in event A
3. Then P(A) = N(A)/N
Mutually exclusivity:
When events A and B have no outcomes in common ![]()
Axioms of probability:
Conditional Probability:
Conditional probability is defined as the likelihood of an event or outcome occurring, based on the occurrence of a previous event or outcome. It is the measure of the probability of an event E, given that another event F has already occurred. Some key points to note here are :
1. P(E|F): Here, E is the event whose probability we are calculating, and F is the event it is conditioned on.
2. "|": Is the symbol used to determine the unknown event (E) and the conditioning event (F).
3. P(F) > 0: The probability of the conditioning event must be positive, otherwise the conditional probability is undefined.
Baye's Theorem Derivation: Starting with the definition of Conditional Probability
In Step 1 with the definition of conditional probabilities, it is assumed that P(A) and P(B) are not 0.
In Step 2 we multiply both sides by P(B) and in step 3 we multiply both sides by P(A) and we end up with the same result on the right hand side of each.
In Step 4 we are able to set both left sides equal to each other since they both have the same right hand side.
In Step 5 we divide both sides by P(B) and we arrive at Baye's Theorem.
It is also important to introduce the law of total probability:
The law of total probability is commonly used in Baye's rule. It is very useful, because it provides a way to calculate probabilities by using conditional probabilities. This is used commonly to compute the denominator when given partitions of the conditional probabilities. A quick example using the law of total probability is:
In this example we are able to solve for the probability of A by just using the probability of A given B, the probability of A given the complement of B, and the probability of B.
Baye's Disease Example: