Types of Riemann Surfaces
It is easier to wrap one’s head around the idea of Riemann surfaces with some discrete examples. There are many different types of surfaces that can be classified as Riemann Surfaces. This section will explore a few examples of Riemann Surfaces between the most simple to more complicated surfaces.
The Riemann Sphere
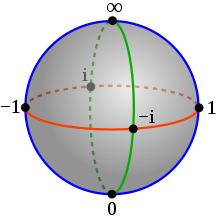
The first example of a Riemann Surface to understand is the Riemann Sphere. It models the complex plane, but extends it, adding a point for zero and infinity.
The image above is the three dimensional visualization of the Riemann Sphere. On one axis, it goes from -1 to 1 and on another, -i to i, representing the complex plane. The third axis goes from 0 to ∞ on what is considered the z-axis. We think of the boundary of the sphere as a complex version of the function f(x) = 1/x. With this sphere, the function behaves nicely since there is a defined path between zero and the infinity point. Usually, the function’s limit can’t be found at zero since it goes to negative infinity from the left and positive infinity from the right, but by through the Riemann Sphere, going left or right from zero both end up at infinity making the equations 1/∞ = 0 and 1/0 = ∞ true.
Complex Torus
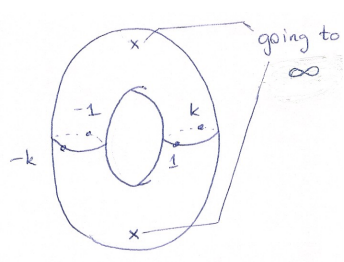
A complex torus is somewhat difficult to imagine at first thought. It is the same in shape as a regular torus, which looks like a doughnut. For the complex version, we think of a function w2 = z where w and z are complex, making the surface S={(z,w)ℂ2| w2=z}(Teleman, C). As with most Riemann Surfaces, we focus on how a function like w acts on a surface, rather than trying to understand it as a multi-valued function in multiple dimensions. This equation is expanded to where:
This new function w has real values for z < -k, -1 < z < 1, and z > k given that k is a complex number and k ≠ 1. Between -1 and 1, the function looks like an ellipse and acts like a square root when less than -k or greater than k. This tells us that we have discrete values of w for all values between -1 and 1, which makes up the interior boundary of the torus. The inside of the torus must be the parts where -k < z < -1 and 1 < z < k since w is imaginary there. The outer boundary is the most difficult to visualize. Following as z increases past k towards infinity or decreases past -k towards negative infinity, w will begin to approach positive and negative infinity. For the purpose of making a surface, the sign of the infinity doesn’t matter and we connect the infinite values of w at two points, the loop between them defining the outer boundary of the torus, making a surface whose thickness is dependent on the value of k. A sketch of the complex torus is shown below.
Hyperelliptic Curves
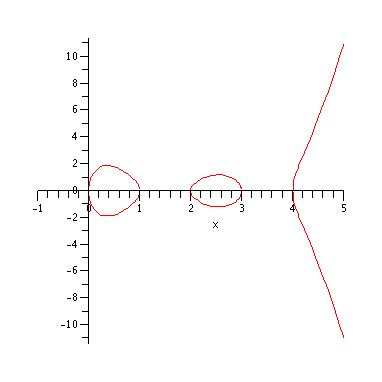
A hyperelliptic curve is one of the most simple Riemann Surfaces since it is only defined by an algebraic curve. This surface is characterized by a genus greater than or equal to 2. A genus is a “hole” in the surface. Think of how a torus has a hole in the middle of it, giving it the donut shape. A torus has one genus. A hyperelliptic curve has two or more holes in it, meaning it has a genus ≥ 2, making it look like a “donut” with two holes in it. On a two dimensional level, a hyperelliptic curve looks like something in the image below (Arapura, n.d.). Notice the two ellipses that do not overlap; they are hyperelliptic as both curves have a curvature of -1 as they face each other.
When this curve is mapped to the complex plane by a map that is degree two (the function that translates from the surface to the complex plane), a multi-holed torus surface is given. This would make sense that a map like this would induce a curved complex structure as the path to get from the plane w to the branches above it would be curved and distorted in space, forming this hyperelliptic curved surface. In other words, the surface induced by the complex plane from this hyperelliptic curve is this torus with more than one hole.
The function that defines this curve can be related to its genus since the function that defines this curve will have roots of 2g + 1 or 2g + 2 (g being the genus ≥ 2). The Riemann Surfaces is also defined as having 2g - 1 geodices (which are lines that are warped by the shape and curvature of the surface) that all intersect at one point exclusively, meaning they do not overlap anywhere else. These characteristics along with a map that has a degree equal two 2, a hyperelliptic Riemann surface can be formed.