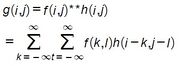Image Convolution with Different Filter Applications
The convolution of an image is basically the same process as signal convolution. The filter matrix needs to be flipped both horizontally and vertically then applied to the image matrix. We add the product of the flipped filter matrix together to get the value of that pixel of the filtered image. This process is explained below:
Different filters have different usages: they can be used to smooth images, sharpening images, and detect image edges.
Image smoothing:
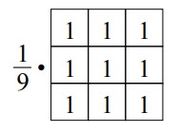
Mean filter: The figure shown below is the example of a mean filter, which is the simplest kind of filter. If we apply the filter to the image, it will add the value of one pixel and 8 other pixels around it together and divide the sum by nine. What it does to the image is reduce the difference of the value of one pixel with the values of the pixels around it.
Gaussian filter: The Gaussian filter is another kind of image smoothing filter, which has a very good result in spatial and spectral localization characteristics. The gaussian filter has the form of the function shown below:
σ 2 is the variance, which determines the size of pass band area. C is applied here to make sure that the sum of the filter coefficients is one. The matrix shown below is a Gaussian filter with the size of 5*5 and variance 1:
0.0030 0.0133 0.0219 0.0133 0.0030 0.0133 0.0596 0.0983 0.0596 0.0133 0.0219 0.0983 0.1621 0.0983 0.0219 0.0133 0.0596 0.0983 0.0596 0.0133 0.0030 0.0133 0.0219 0.0133 0.0030
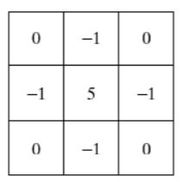
Image sharpening: Image sharpening is used to enhance image details. The figure shown below is an example of an image sharpening filter.
This filter is used to make the difference between the value of the pixel in the middle and the valued of the pixels around it more apparent, which means the edge of that pixel will be sharper.
Edge detection: An edge can be defined as a set of contiguous pixel positions where an abrupt change of intensity (gray or color) values occur. Edge detection is commonly used in image processing. The general idea of this is to use the gradient of the pixels to help identify whether or not it is an edge.
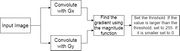
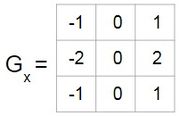
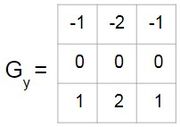
Sobel edge detection: Sobel edge detection probably is the most widely known edge detection method. The process and filters are shown below:
Gx and Gy are shown in the figure above. When these filters are convoluted with an area on an image without edges, it will result in a very small value because the differences of the images are so small that the equation would not detect it. When the filters are shifted to places where there are edges, things would be different. For Gx, if the edge is horizontal, it will not be detected since the convolution will be zero. But if the edge is vertical, the value of the edge will be much larger. For Gy, if the edge is vertical, it will not be detected since the convolution will be a small value. But if the edge is horizontal, the value of the edge will be much larger. After the convolution of the image with both of the filters, there will be two matrices with positive and negative values, large and small. Next, the two new matrices are used in function listed below:
the outcome will be a matrix with only positive values, some big and some small. Now after applying a threshold, the values larger than the threshold will be set to 255, and values smaller than the threshold to zero. If thresholds are not used, the edges will not be very noticeable except for the prominent edges.