Introduction
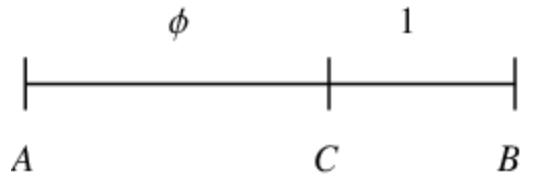
The golden ratio is a ratio such that, given two quantities a and b,
The golden ratio, $ \phi $, is sometimes also called the golden mean or the golden section. The golden ratio can be frequently observed in man-made objects, though they are generally “imperfectly golden” – that is, the ratio is approximately the golden ratio, but not exactly. Some everyday examples include: credit cards, $ \frac{w}{h}=1.604 $, and laptop screens, $ \frac{w}{h}=1.602 $ (Tannenbaum 392).
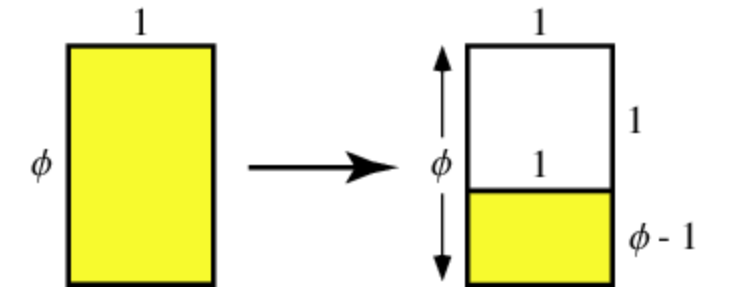
Visualizations of the golden ratio can be seen below (Weisstein):
MathIsFun also has an interactive display that can construct a rectangle in the golden ratio given a certain fixed width or length.