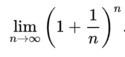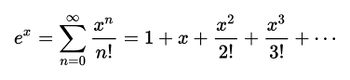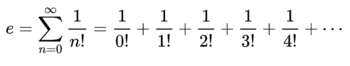Defining e
There are a number of constants in mathematics that are defined by geometry in some way. For example, Archimedes' constant π is defined as the ratio between the circumference and diameter of a circle. Pythagoras' constant sqrt(2) is defined as the length of the diagonal of a square with sides of 1. However, e is based on formulae rather than geometry.
When Jacob Bernoulli was studying compound interest in 1683, his work led him to a formula:
Let's observe what happens to the value of the formula when different values of n are used:
| n | (1+1/n)^n |
|---|---|
| 5 | 2.48832 |
| 50 | 2.69159 |
| 100 | 2.70481 |
| 100,000 | 2.71827 |
| 1,000,000 | 2.71828 |
As can be seen from the table, the value of the formula converges towards a constant number, which in this case is e. Therefore, we can see that Bernoulli's formula is one way to calculate the value of e.
Leonhard Euler was the one who defined this constant with the symbol e in one of his papers in 1731. He proved that the constant was irrational by finding a formula that was never ending, thereby proving it was irrational. He was also able to find the first 18 digits of e using a different formula he came up with to define the number. This particular formula is based on the Taylor Series of ex. The Taylor Series of ex is:
Since e is the same as taking x=1 in the series, we get the following formula for e:
Therefore, we can see another way of calculating the value of e. Bernoulli's formula is more complicated since the numbers can get complicated quickly because of taking powers of irrational numbers. But Euler's formula is much simpler since it uses relatively common fractions and addition to find the value.