Answers and Discussions for
Contents
Problem 1
Create and Solve Magnetic Equivalent Circuit
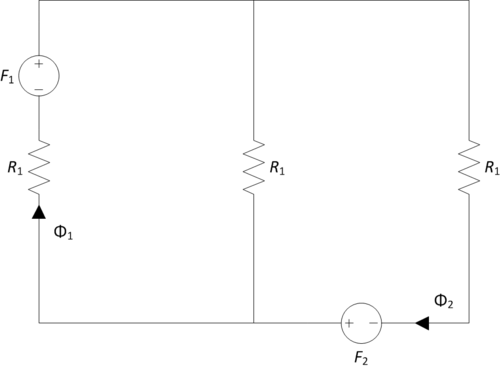
A magnetic equivalent circuit (MEC) needs to be constructed from the given EE core inductor geometry. A magnetomotive force (MMF) with general form $ \mathcal{F} = Ni $ acts as an analogue of an independent voltage source. In general, a reluctance may be expressed as $ \mathcal{R} = \frac{\ell}{\mu A} $ and function as a resistance analogue. If the steel has high permeability, then the reluctance associated with a path through steel is small (real conductor equivalent). In this problem, the permeability of air (linear, isotropic, and homogeneous) is treated as free space: $ \mu_{\text{air}} = \mu_{r,\text{air}} \mu_0 \approx \mu_0 $. Without any fringing or leakage considered, magnetic flux $ \Phi $ will more or less follow the direction of the steel.
The magnetomotive forces are straightforward expressions of turn count and current.
- $ \mathcal{F}_1 = N_1 i_1 $
- $ \mathcal{F}_2 = N_2 i_2 $
The reluctance needs to be calculated using the length and cross sectional area presented to the path in the air gap. $ \mathcal{R}_1 = \frac{g}{\mu_0 w \ell} $
The total magnetic flux passing through $ \mathcal{F}_2 $ needs to be found. Because all the reluctances are independent of magnetic flux, the linear circuit technique of superposition may be used. Let $ \Phi_{1,only} $ be the magnetic flux through $ \mathcal{F}_1 $ with $ \mathcal{F}_2 = 0 $ (magnetic short circuit). Similarly, let $ \Phi_{2,only} $ be the magnetic flux through $ \mathcal{F}_2 $ with $ \mathcal{F}_1 = 0 $. Similar to current division, magnetic flux division is used to find the magnetic flux in the xth branch $ \Phi_x $ of $ K $ branches that receive the total magnetic flux $ \Phi_{tot} $ (KCL equivalent): $ \Phi_x = \frac{\sum_{k \in \{1, 2, ..., K\} \setminus \{x\}} \mathcal{R}_k}{\sum_{k \in \{1, 2, ..., K\}} \mathcal{R}_k} \Phi_{tot} $.
$ \begin{align} \Phi_2(i_1,i_2,g) &= \Phi_{1,only} \frac{\mathcal{R}_1}{\mathcal{R}_1 + \mathcal{R}_1} + \Phi_{2,only} \left(1\right) \\ \Phi_2(i_1,i_2,g) &= \frac{\mathcal{F}_1}{\mathcal{R}_1 + \frac{1}{2} \mathcal{R}_1} \left(\frac{1}{2}\right) + \frac{\mathcal{F}_2}{\mathcal{R}_1 + \frac{1}{2} \mathcal{R}_1} \\ \Phi_2(i_1,i_2,g) &= \frac{N_1 i_1}{\frac{3}{2} \mathcal{R}_1} \left(\frac{1}{2}\right) + \frac{N_2 i_2}{\frac{3}{2} \mathcal{R}_1} \\ \Phi_2(i_1,i_2,g) &= \frac{N_1 i_1}{3\mathcal{R}_1} + \frac{2N_2 i_2}{3\mathcal{R}_1} \\ \Phi_2(i_1,i_2,g) &= \frac{\mu_0 w \ell}{3 g} \left(N_1 i_1 + 2N_2 i_2\right) \end{align} $
The magnetic flux linkage of the second coil follows readily.
$ \begin{align} \lambda_2(i_1,i_2,g) &= N_2 \Phi_2(i_1,i_2,g) \\ \lambda_2(i_1,i_2,g) &= \frac{\mu_0 w \ell}{3 g} \left(N_1 N_2 i_1 + 2N_2^2 i_2\right) \end{align} $
Voltage Calculation
The current waveforms are $ i_1(t) = I_1 \cos(\omega_e t) $ and $ i_2(t) = I_2 \cos(\omega_e t) $ where $ I_1 = 10 \, \text{A} $, $ I_1 = 40 \, \text{A} $, and $ \omega_e = 100 \, \frac{\text{rad}}{\text{s}} $. The airgap distance $ g $ remains fixed.
The voltage equation for the second coil may be written down (winding resistance is negligible).
$ \begin{align} v_2(t) &= \cancelto{0}{r_2} i_2(t) + \mathit{p}\lambda_2(t) \\ v_2(t) &= \frac{\mu_0 w \ell}{3 g} \frac{d}{dt} \left[N_1 N_2 i_1(t) + 2N_2^2 i_2(t)\right] \\ v_2(t) &= \frac{\mu_0 w \ell}{3 g} \frac{d}{dt} \left[N_1 N_2 I_1 \cos(\omega_e t) + 2N_2^2 I_2 \cos(\omega_e t)\right] \\ v_2(t) &= -\frac{\mu_0 w \ell}{3 g} \omega_e \left[N_1 N_2 I_1 \sin(\omega_e t) + 2N_2^2 I_2 \sin(\omega_e t)\right] \\ v_2(t) &= -\frac{\left(4\pi \times 10^{-7} \, \frac{\text{H}}{\text{m}}\right) \left(\frac{1}{40} \, \text{m}\right) \left(10^{-1} \, \text{m}\right)}{3 \left(\pi \times 10^{-3} \, \text{m}\right)} \left(10^2 \, \frac{\text{rad}}{\text{s}}\right) \left[\left(10^4\right) \left(10 \, \text{A}\right) + \left(2 \times 10^4\right) \left(40 \, \text{A}\right)\right] \sin\left(100 \, \frac{\text{rad}}{\text{s}} \cdot t\right) \\ v_2(t) &= -\frac{\left(\cancel{4}\cancel{\pi} \times 10^{-7} \, \frac{\text{H}}{\text{m}}\right) \left(\frac{1}{\cancelto{10}{40}} \, \text{m}\right) \left(10^{-1} \, \text{m}\right)}{3 \left(\cancel{\pi} \times 10^{-3} \, \text{m}\right)} \left(10^2 \, \frac{\text{rad}}{\text{s}}\right) \left[9 \times 10^5 \, \text{A}\right] \sin\left(100 \, \frac{\text{rad}}{\text{s}} \cdot t\right) \\ v_2(t) &= -30 \sin\left(100 \, \frac{\text{rad}}{\text{s}} \cdot t\right) \, \text{V} \end{align} $
The answer to this problem is mostly substitution, a time derivative of a sinusoid, and careful evaluation of the numerical value.
$ \begin{equation} \boxed{v_2(t) = -30 \sin\left(100 \, \frac{\text{rad}}{\text{s}} \cdot t\right) \, \text{V}} \end{equation} $