1)
Changing $ \bar{B} $ will include $ \bar{E} $ which rotates wheel
$ \nabla\times\bar{E} = -\frac{\partial }{\partial t}{\bar{B}}\text{ \underline{where:} }\bar{B} = B_0\mu(-t)\text{ step function } $
$ \oint \bar{E}\cdot d\bar{l} = - \frac{\partial }{\partial t}\int_S\bar{B}\cdot ds $ $ \int_0^{2\pi}E_\phi \rho d\phi= B_0(\pi a^2)\delta(t) $ $ \bar{E}_\phi = \frac{B_0(\pi a^2)}{2\pi \rho} = \frac{B_0a^2}{2\rho}\delta(t) $ $ \bar{E}=\frac{B_0a^2}{2\rho}\delta(t)\hat{\phi} $ $ \bar{F} = q[\bar{E}+\bar{\mu}\times\bar{B}]=q\bar{E}=(2\pi R)\lambda\bigg(\frac{B_0a^2}{2R}\bigg)\delta(t)\hat{\phi} $ $ \bar{F}=\pi\lambda B_0a^2\delta(t)\hat{\phi} $ $ \tau=\bar{r}\times\bar{F}= RF\sin\theta=RB_0\lambda(\pi a^2)\delta(t)=\frac{dL}{dt} $ $ L=RB_0\lambda(\pi a^2) $ ------------------------------------------------------------------------------------ 2)$ \bar{J}=\sigma\bar{E}: \nabla\times\bar{E} = -\frac{\partial B}{\partial t}\hspace{1cm}\nabla\times\bar{H}= \bar{J}+\frac{\partial D}{\partial t} $
$ \varepsilon_0(t)= L\frac{di(t)}{dt}+Ri(t)=\varepsilon_0\mu(t) $
$ e^{R/Lt}\bigg[ \frac{di(t)}{dt}+\frac{R}{L}i(t)=\frac{\varepsilon_0}{L}\mu(t)\bigg] $
$ \frac{d}{dt}\bigg[e^{R/Lt}i(t)\bigg] = \frac{\varepsilon_0}{L}e^{R/Lt}\mu(t) $
$ e^{R/Lt}i(t) = \int_0^t\frac{\varepsilon_0}{L}e^{R/Lt`}\mu(t`)dt`=\frac{\epsilon_0}{R}e^{R/Lt}-\frac{\epsilon_0}{L} $
$ i(t) = \frac{\epsilon_0}{R}-\frac{\epsilon_0}{R}e^{-R/Lt} $
------------------------------------------------------------------------------------
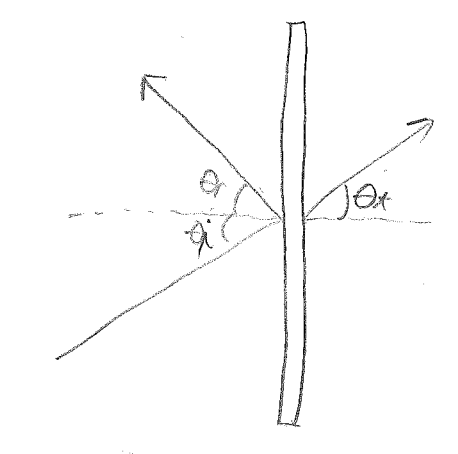
3)
\underline{want:}$ \Gamma = -1,T=0 $
for critical angle: $ \theta_t=\frac{\pi}{2} $
$ n_1\sin\theta_i = n_2\sin\theta_t $
$ \sin\theta_c = \frac{n_2}{n_1}\sin\bigg(\frac{\pi}{2}\bigg) = \frac{n_2}{n_1} $
$ \theta_c =sin^{-1}\bigg(\frac{n_2}{n_1}\bigg) = sin^{-1}\bigg(\frac{\sqrt{\epsilon_{r2}}}{\epsilon_{r1}}\bigg) $
\underline{for region 2:}
$ \nabla\times\bar{H} = \bar{J}+\frac{\partial D}{\partial t} = (\sigma+j\omega\epsilon)\bar{E} $
$ \epsilon_c = \big(\epsilon+\frac{\sigma}{j\omega}\big)\text{ where: }\sigma(\Omega/m)\approx N $
$ \sqrt{\epsilon_{r2}} = \sqrt{\epsilon_{c2}} = \sqrt{\epsilon_{r2}+\frac{\sigma}{j\omega}} $
for PEC: $ \sigma\to\infty $ and $ -90\le\theta_c\le90 $
\underline{textbook(plasma):} $ f_p = \frac{1}{2\pi}\sqrt{\frac{Ne^2}{m\epsilon}}\text{ cheng 374 } $
$ \to\epsilon_p = \epsilon_0\bigg(1-\frac{f_p^2}{f^2}\bigg) $
$ \theta_c = sin^{-1}(\sqrt{\epsilon_p}) $