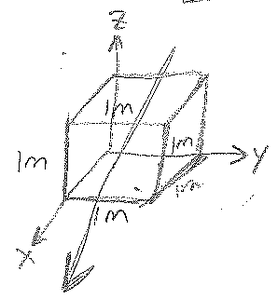
$ \begin{align*} \nabla \cdot \bar{D} &= \rho \\ \quad (\frac{\partial}{\partial x}\hat{x}+\frac{\partial}{\partial y}\hat{y}+\frac{\partial}{\partial z}\hat{z})\cdot(2\hat{x})&=\rho \\ \frac{\partial}{\partial x}(2)&=0=\rho \quad \text{(no charge)} \end{align*} $
Also:
$ \begin{align*} \oint \bar{D}\cdot d\bar{S}&=Q\\ &=\int2(dS_x)+\int2(-dS_x)=2-2=\boxed{0} \end{align*} $