Downsampling
A slecture by ECE student Yerkebulan Yeshmukhanbetov
Partly based on the ECE438 Fall 2014 lecture material of Prof. Mireille Boutin.
Contents
Outline
- Introduction
- Definition of Downsampling
- Derivation of DTFT of downsampled signal
- Example
- Conclusion
- References
Introduction
This slecture provides definition of downsampling, derives DTFT downsampled signal and demonstrates it in a frequency domain. Also, it explains process of decimation and why it needs a low-pass filter.
Definition of Downsampling
Downsampling is an operation which involves throwing away samples from discrete-time signal. Let x[n] be a digital-time signal shown below:
GRAPH
then y[n] will be produced by downsampling x [n] by factor D = 3. So, y [n] = x[Dn].
GRAPH
As seen in above graph, y [n] is obtained by throwing away some samples from x [n]. So, y [n] is a downsampled signal from
x [n].
Derivation of DTFT of downsampled signal
Let x (t) be a continuous time signal. Then x1 [n] = x (T1n) and x2 [n] = x (T2n). And ratio of sampling periods would be
D = T2/T1, which is an integer greater than 1. From these equations we obtain realtionship between x1 [n] and x2 [n].
$ \begin{align} x_2 [n] = x(T_2 n) = x(DT_1 n) = x_1 [nD] \end{align} $
Below we derive Discrete-Time Fourier Transform of x2 [n] in terms of DTFT of x1 [n].
$ \begin{align} &\mathcal{X}_2(\omega)= \mathcal{F}(x_2 [n]) = \mathcal{F}(x_1 [Dn])\\ &= \sum_{n = -\infty}^\infty x_1[Dn] e^{-j \omega n} = \sum_{m = -\infty}^\infty x_1[m] e^{-j \omega {\frac{m}{D}}}\\ &= \sum_{n = -\infty}^\infty s_D[m]* x_1 [m] e^{-j \omega {\frac{m}{D}}}\\ \end{align} $
where
$ s_D [m]=\left\{ \begin{array}{ll} 1,& \text{ if } n \text{ is a multiple of } 4,\\ 0, & \text{ else}. \end{array}\right. = {\frac{1}{D}} \sum_{k = -\infty}^{D-1} e^{jk {\frac{2 \pi}{D} m}} $
$ \begin{align} &\mathcal{X}_2(\omega)= \sum_{m = -\infty}^\infty {\frac{1}{D}} \sum_{k = -\infty}^{D-1} e^{jk {\frac{2 \pi}{D} m}} x_1[m] e^{-j \omega {\frac{m}{D}}}\\ &= {\frac{1}{D}} \sum_{k = -\infty}^{D-1} \sum_{m = -\infty}^\infty x_1[m] e^{-jm ({\frac{\omega - 2 \pi k}{D}})} = \\ &= {\frac{1}{D}} \sum_{k = -\infty}^{D-1} \mathcal{X}_1 ({\frac{\omega - 2 \pi k}{D}}) \\ \end{align} $
Example
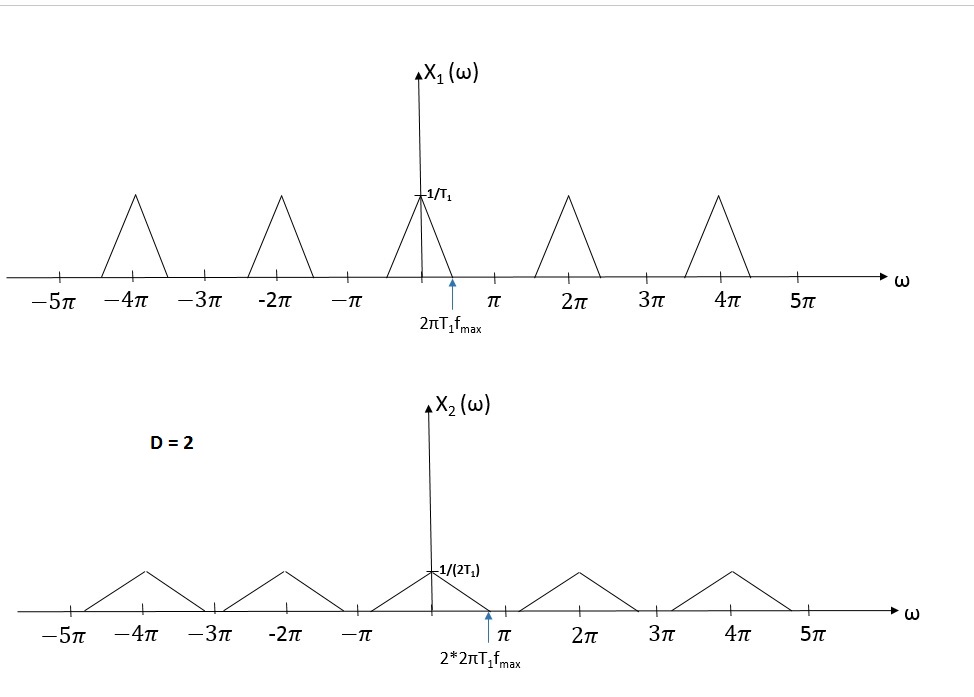
Let's take a look at an original signal X1 (w) and X2 (w) which is obtained after downsampling X1(w) by factor D = 2 in a frequency domain.
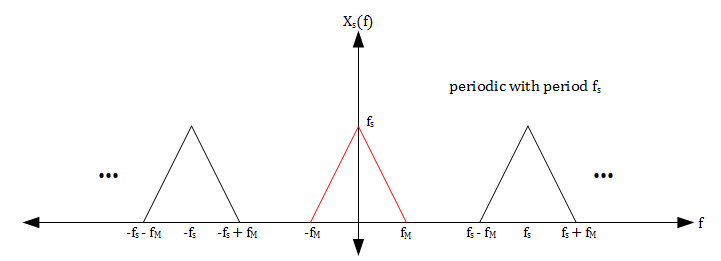
We would like to determine what Xs(f) looks like in order to find a way to reconstruct x(t).
Since we have sampled at a rate fs > 2fM, the following inequalities hold:
$ f_s > 2f_M \iff f_s - f_M > f_M \iff -f_s + f_M < f_M $.
Together, these inequalities, the graph of X(f), and the expression for Xs(f) in terms of X(f) imply that Xs(f) will have the spectrum shown in the figure below.
Notice that the spectrum of the ideal sampling of a signal is an amplitude scaled periodic repetition of the original spectrum. Since x(t) is bandlimited and we have sampled at a rate fs > 2fM, the periodic repetitions of X(f) do not overlap.
All the information needed to reconstruct X(f) can be found in the portion of Xs(f) that corresponds to X(f) (shown in red). Therefore we can use a simple lowpass filter with gain $ \tfrac{1}{f_s} $ and cutoff frequency $ \tfrac{f_s}{2} $ to recover X(f) from Xs(f).
$ X(f) = X_s(f)\left\{ \begin{array}{ll} \frac{1}{f_s}, & |f| \le \frac{f_s}{2}\\ 0, & \text{else} \end{array} \right. $
$ \iff x(t) = x_s(t)*\text{sinc}(f_st) $
$ \therefore $ We can perfectly reconstruct x(t) from xs(t).
Example
Though the Nyquist theorem states that perfect reconstruction is possible if we satisfy the Nyquist condition (fs > 2fM), it is important to note that this condition is not necessary. The following example demonstrates how perfect reconstruction is sometimes possible even when undersampling.
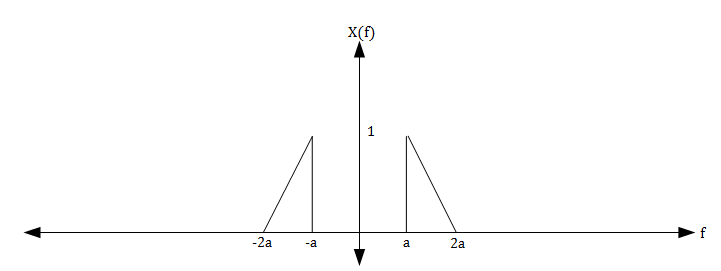
Let the signal x(t) have a spectrum X(f) as seen in the figure below.
The Nyquist condition states that we should sample at a rate fs > 2(2a) = 4a. Instead, let us sample at fs = 2a.
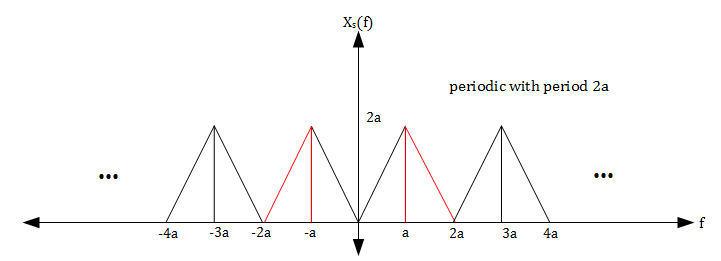
As before, we have $ x_s(t) = x(t)p_{\frac{1}{f_s}}(t) $ and $ X_s(f) = f_s\sum_{k = -\infty}^\infty X(f-kf_s) $
$ \implies X_s(f) = 2a\sum_{k = -\infty}^\infty X(f-2ka) $.
Therefore, Xs(f) will have the spectrum shown in the figure below.
Notice that there is no aliasing in Xs(f) even though fs < 4a. In addition, the portion of Xs(f) that corresponds to X(f) (shown in red) can be recovered using a bandpass filter with gain $ \tfrac{1}{2a} $ and cutoff frequencies a and 2a.
Conclusion
To summarize, the Nyquist theorem states that any bandlimited signal can be perfectly reconstructed from its sampling if sampled at a rate greater than twice its bandwidth (fs > 2fM). However, the Nyquist condition is not necessary for perfect reconstruction as shown in the example above.
References
[1] John G. Proakis, Dimitris G. Manolakis, "Digital Signal Processing with Principles, Algorithms, and Applications" 4th Edition,2006
Questions and comments
If you have any questions, comments, etc. please post them on this page.