Fourier Transform rep com Youqin Liu ECE438 slecture - Rhea

ECE438 SELECTURE

1.INTRODUCTION:

The topic 3 is the Fourier Transform of the Comb and Rep function. In my selecture, I am going to introduce the definition, the Fourier Transformation and the relationship of Comb function and Rep function.

2.THEORY:

(1)

Reference:https://engineering.purdue.edu/~bouman/ece637/notes/pdf/RepComb.pdf

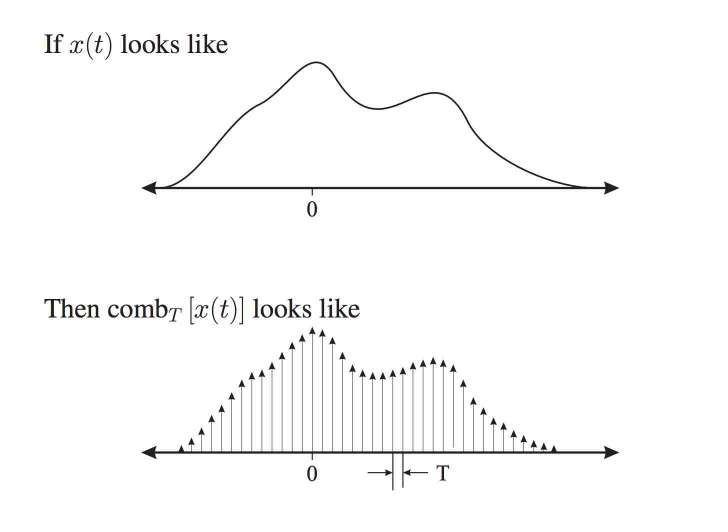
According to the definition of the comb function:

$ comb_T\big(X(t)\big)= x(t)\cdot\ P_T(t) $

where $ P_T(t)= \sum_{n=-\infty}^\infty \delta(t-nT) $

Do the Fourier Transform to the function:

$ F\bigg(comb_T\big(x(t)\big)\bigg) = F\big(x(t)\cdot P_T(t)\big) $

According to the property of Fourier Transformation, the multiplication in the time domain is equal to the convolution in the frequency domain.

$ F\bigg(comb_T\big(x(t)\big)\bigg) = F\big(x(t)\big)* F\big(P_T(t)\big) $

                 $ =x(f)*F\big(P_T(t)\big) $

Because $ P_T(t)= \sum_{n=-\infty}^\infty \delta(t-nT) $ is a periodic function , so we can expand it to Fourier series.

$ P_T(t)=\sum_{n=-\infty}^\infty F_n e^{jn\cdot 2\pi t/T}  $

$ \Rightarrow F_n = \frac{1}{T}\int\limits_{-T/2}^{T/2}P_T(t)e^{jn\cdot 2\pi t/T}dt $

      $ =\frac{1}{T} $

So, $ P_T(t) = \frac{1}{T}\sum_{n=-\infty}^\infty F_n e^{jn\cdot 2\pi t/T} $

         $ =\sum_{n=-\infty}^\infty \frac{1}{T} F(e^{jn\cdot 2\pi t/T})  $

         $ =\sum_{n=-\infty}^\infty \frac{1}{T} \delta(f-\frac{n}{T}) $

         $ = \frac{1}{T}P_{1/T}(f) $

So, $ F\bigg(comb_T\big(x(t)\big)\bigg)=X(f)*\frac{1}{T}P_{1/T}(f) $

                    $ =\frac{1}{T}X(f)*P_{1/T}(f) $
  
                    $ =\frac{1}{T}rep_{1/T}X(f) $

--- (2)

Reference:https://engineering.purdue.edu/~bouman/ece637/notes/pdf/RepComb.pdf

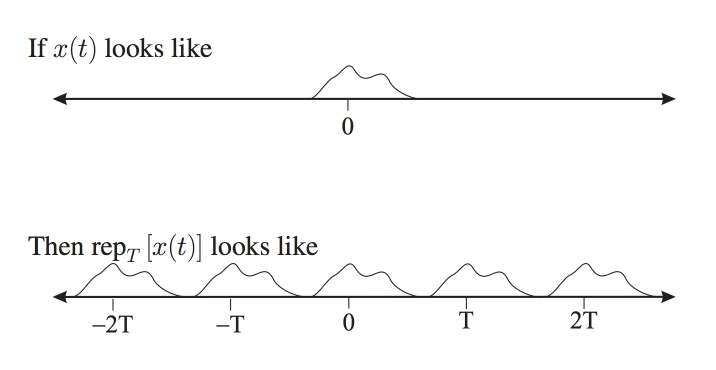
According to the definition of Rep function:

        $ rep_T\big(x(t)\big):= x(t)*P_T(t) $

                   $ =x(t)*\sum_{n=-\infty}^\infty \delta(t-nT) $

So, $ F\bigg(rep_T\big(x(t)\big)\bigg)=F\bigg(x(t)*\sum_{n=-\infty}^\infty \delta(t-nT)\bigg) $

Use the impluse-train we get previously, according to the conclusion we get from Fourier Transformation of it, we know:

         $ F\big(P_T(t)\big)=\frac{1}{T}P_{1/T}(f) $

So, $ F\bigg(rep_T\big(x(t)\big)\bigg)=x(f)\cdot\frac{1}{T}P_{1/T}(f) $

                   $ =\frac{1}{T}x(f)\cdot P_{1/T}(f) $ 

(create a question page and put a link below)

Questions and comments

If you have any questions, comments, etc. please post them on this page.

Back to ECE438, Fall 2014