Any integer factors, more or less uniquely, into prime numbers. Does this question make sense for real numbers? What about numbers of the form a+b*i where i^2=-1 and a,b are integers? What about numbers of the form a+b*root(N) where a,b,N are integers?
(Possible appendix: What does this concept have to do with Fermat's Last theorem, and what does FLT say anyway?)
Unique Factorization: by Brooke Wilke, Jerad Stump, Rachel Aker, Brandon Myers, Kayla Kerker
First, what is Unique Factorization? The unique factorization theorem is also known as the Fundamental Theorem of Arithmetic which states that all integers greater than 1 are either prime numbers or can be created by multiplying prime numbers.
Mathisfun.com provides a great picture of what this looks like:
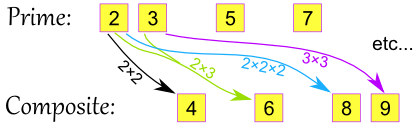
Let's begin with defining what an integer is. An integer consists of all natural numbers (0,1,2,...), includes 0 and all all of the natural numbers of the opposite signs (-1,-2,....). In order to further our understanding of unique factorization, we must also define a prime number. A prime number according to Webster's dictionary is "a number (such as 2, 3, or 5) that can only be exactly divided by itself and by 1". In other words, a prime number is a number with no factors beyond itself or 1.
In this project, we will be explaining how every integer greater than 1 factors into a unique set of prime numbers, and later we will discuss whether this concept with also suffice for real, imaginary and/or rational numbers as well.
The Real Numbers:
The real numbers include all numbers from negative infinity to positive infinity. Examples of real numbers: 1,4,8, 4/5,(2)1/2, -10 are all considered real numbers.
Using the fundamental theorem of arithmetic which states: every integer greater that 1 can be written uniquely as a prim or as the product of two or more primes where the prime factors are written in order of nondecreasing size.
In lay term this is saying you can break down any number that is not a prime number in to products of primes. Also it is saying that no matter how you factor a number that number will factor the same every time and down to the same prime numbers.
An example of this is if you have the number 480 broken down into primes looks like this: 2*2*2*2*2*3*5 or 25*3*5 both are correct forms for the breakdown of 480. No matter how many ways you do the factoring you will always have five 2’s, one 3, and one 5.
Now the theorem states that for every integer greater thar than one and not prime the factorization is unique or that no two numbers have the same factorization. For the exact theorem please see http://www.math.hawaii.edu/~lee/courses/fundamental.pdf which is the University of Hawaii proof.
The negative integers less than -1 we can say the same thing that they will have the same uniqueness as the positive. Mainly because -480 will have the same factorization but with a negative number or three in the factorization. So those will have a unique factorization as well.
Now we have covered integers that are greater than 1 so we must talk about -1, 0, and 1 which we don't really care about. The reason we don't care too much is because 1 times anything is itself is itself and the same goes for -1. Now 0 is excused because you really can't do much with 0.
The other categories in the reals excluding the imaginary which will be covered in the next section. Have inverses and anything with an inverse can be ruled out and will have a unique factorization. This is hard to understand why this holds but mainly due to fields and what this paper from Harvard states http://math.harvard.edu/~waffle/ufds2.pdf.
Unique Factorization and Complex Numbers
The unique factorization property can be formulated in any integral domain. Consider the ring Z[i] of Gaussian integers. Here i=√(-1), and the easiest way to view Z[i] is as the subring of complex numbers {a+bi│a,b∈Z} . For more information on rings and subrings proceed to: http://www.rowan.edu/open/depts/math/howe/BookChapters/Subrings%20&%20Ideals.pdf
What would it even mean for Z[i] to have unique factorization? We would like to have a notion of “primes" in this ring. Our definition for a real prime, of a nonzero element which is only divisible by 1 and itself, doesn't quite work, since every a+bi "is divisible by" ±i: a + bi = i(b- ai)= -i(-b + ai) One might think to define “positive" Gaussian integers as those a+bi with a,b > 0, i.e., those in the first quadrant of C but this notion of positivity isn't stable under multiplication: (1 + i)^2= 2i,(i + 1)^4=-4 In fact there is no ordering on Z[i] compatible with its ring structure in a sense which we make precise in the exercises. It turns out we need to regard the four integers ±a+bi,±i(a+bi) as being in some sense equivalent, just as we regard ±n as being in some sense equivalent in Z.
Two key questions to ask are: Q1: Does every (nonzero nonunit) x∈Z[i] admit a factorization into irreducibles? Q2: If so, is the irreducible factorization essentially unique, in the sense that if x = p_1⋯p_r=q_1⋯q_s are two irreducible factorizations, then there exists a one-to-one correspondence σ:{1,…,r}→{1,…,s} such that for all 1≤i≤r,p_i and σ(p_i) are associates? For more information on associates, proceed to: http://planetmath.org/associates
The first question is answered intuitively: consider a nontrivial factorization x=yz. The two factors get “smaller” i.e. the length of x is precisely the length of y times the length of z, and the nonzero nonunits are precisely the elements a + bi "of" Z[i] "whose length" √(a^2+b^2 ) is greater than 1. Thus, if x = yz is a nontrivial factorization, then indeed y and z have smaller lengths than x.
This doesn't mean that the factorization process has to stop, because the length is a real number, and there is no smallest real number, nor a smallest real number which is greater than 1. We call the norm of a+bi,N(a + bi)= a^2+b^2.
Therefore we have the following criterion for testing the nontriviality of a factorization: z = xy is a nontrivial factorization in Z[i] iff N(z) = N(x)N(y) is a nontrivial factorization in Z "iff" N(x),N(y) > 1. The factorization process will eventually terminate: at each stage the norms get smaller, and the smallest possible value is N(x) = 2.
Unique Factorization in a PID
First make the following definition: a principal ideal domain (PID) is a commutative ring without zero divisors in which every ideal is principal.
Theorem: Let R be a PID, and let x be a nonzero nonunit of R. Then any two irreducible factorizations x = p_1⋯p_r=q_1⋯q_s of x are equivalent in the above sense: there is a bijective correspondence from the p_i's to the q_j's in which corresponding elements are associates.
Now we recall Euclid's Lemma in R. It says that if p is an irreducible element of R and p|xy,then p|x or p|y.
Finally, the deduction of the uniqueness of the factorization is again exactly the same, with the small change that since we are only concluding that the primes p_i and q_j are associates, when we cancel p_i and q_j we have to correct by a unit. Now we have shown every PID is a UFD.
The Gaussian integers form a PID
Let us now establish the key fact: namely that every ideal in Z[i] is principal. As above, since we have already explained that the properties of the norm map N imply that every Gaussian integer can be factored into irreducibles, this will imply that irreducibles are prime and that every nonzero nonunit Gaussian integer can be factored uniquely into irreducibles.
Recall that every ideal of Z is generated by an element which was ‘smallest" in a reasonable sense. In Z, this sense was just smallest in absolute value. So it is very natural to try to show that every ideal in Z[i] is generated by any of its elements of minimal norm. For this we establish the following important result:
Division Theorem in Z[i]:
Let α,β ϵ Z[i],with β≠0. Then there exist γ,δ ϵ Z[i] such that α=γβ+δ with N(δ)<N(β).
Finally, we prove that Z[i] is a PID using the argument alluded to above: let I be a nonzero ideal of Z[i]. Then the set {N(z)│z∈I\0} is a nonempty set of Z^+ so has a least element n; let z_0 be one (of the four) elements of I with N(z_0) = n. We claim that I = (z_0). Since z_0∈I and I is an ideal, we have(z_0)⊂I. Conversely, let z∈I, and apply the division theorem with α=z,β=z_0: z = γz_0 + δ,where N(δ) < N(z_0) = n, so δ is an element of I of norm smaller than n, meaning δ = 0 "and" z∈(z_0).
Fermat’s Last Theorem
Fermat’s Last Theorem states that for the Diophantine equation x^n + y^n = z^n where x, y, and z are integers has no solutions that are nonzero when n>2.
Background: Around 1637 Fermat claimed to have proven this theorem. He wrote in the margins of one of his books that when n>2 there were no solutions to the Diophantine equation. However, he did not prove his claim. 358 years later Andrew Wiles was able to successfully prove Fermat’s last theorem.
An example of a Proof of n=3: x^3 + y^3 = z^3
x^3 -1=(x-1)(x-t)(x-t^2) where t=e^2πi/3 Let x=x/y Can be rewritten as (x^3)/(y^3) – 1=(x/y -1)(x/y –t)(x/y –t^2) Now multiply both sides b y^3 and y become –y. Can be rewritten as z^3 = x^3 + y^3 = (x+y)(x+ty)(x+(t^2)y)
By looking at the prime factors of the left side of the above equation, it is impossible for it to equal z^3.
Andrew Wiles came up with an extensive proof for all “n” in 1994 and it was later published in 1995.
Resources: Rabinoff, J. (n.d.).Retrieved April 26, 2014, from http://people.math.gatech.edu/~jrabinoff6/mathcamp/lectures.pdf
http://www.mathsisfun.com/numbers/fundamental-theorem-arithmetic.html

