Any integer factors, more or less uniquely, into prime numbers. Does this question make sense for real numbers? What about numbers of the form a+b*i where i^2=-1 and a,b are integers? What about numbers of the form a+b*root(N) where a,b,N are integers?
(Possible appendix: What does this concept have to do with Fermat's Last theorem, and what does FLT say anyway?)
Unique Factorization: by Brooke Wilke, Jerad Stump, Rachel Aker, Brandon Myers, Kayla Kerker
First, what is Unique Factorization? The unique factorization theorem is also known as the Fundamental Theorem of Arithmetic which states that all integers greater than 1 are either prime numbers or can be created by multiplying prime numbers.
Mathisfun.com provides a great picture of what this looks like:
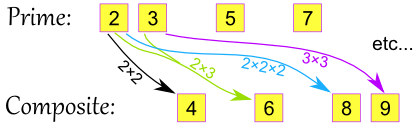
Let's begin with defining what an integer is. An integer consists of all natural numbers (0,1,2,...), includes 0 and all all of the natural numbers of the opposite signs (-1,-2,....). In order to further our understanding of unique factorization, we must also define a prime number. A prime number according to Webster's dictionary is "a number (such as 2, 3, or 5) that can only be exactly divided by itself and by 1". In other words, a prime number is a number with no factors beyond itself or 1.
In this project, we will be explaining how every integer greater than 1 factors into a unique set of prime numbers, and later we will discuss whether this concept with also suffice for real, imaginary and/or rational numbers as well.
The Real Numbers:
The real numbers include all numbers from negative infinity to positive infinity. Examples of real numbers: 1,4,8, 4/5,(2)1/2, -10 are all considered real numbers.
Using the fundamental theorem of arithmetic which states: every integer greater that 1 can be written uniquely as a prim or as the product of two or more primes where the prime factors are written in order of nondecreasing size.
In lay term this is saying you can break down any number that is not a prime number in to products of primes. Also it is saying that no matter how you factor a number that number will factor the same every time and down to the same prime numbers.
An example of this is if you have the number 480 broken down into primes looks like this: 2*2*2*2*2*3*5 or 25*3*5 both are correct forms for the breakdown of 480. No matter how many ways you do the factoring you will always have five 2’s, one 3, and one 5.
Now the theorem states that for every integer greater thar than one and not prime the factorization is unique or that no two numbers have the same factorization. For the exact theorem please see http://www.math.hawaii.edu/~lee/courses/fundamental.pdf which is the University of Hawaii proof.
The negative integers less than -1 we can say the same thing that they will have the same uniqueness as the positive. Mainly because -480 will have the same factorization but with a negative number or three in the factorization. So those will have a unique factorization as well.
Now we have covered integers that are greater than 1 so we must talk about -1, 0, and 1 which we don't really care about. The reason we don't care too much is because 1 times anything is itself is itself and the same goes for -1. Now 0 is excused because you really can't do much with 0.
The other categories in the reals excluding the imaginary which will be covered in the next section. Have inverses and anything with an inverse can be ruled out and will have a unique factorization. This is hard to understand why this holds but mainly due to fields and what this paper from Harvard states http://math.harvard.edu/~waffle/ufds2.pdf.
Fermat’s Last Theorem
Fermat’s Last Theorem states that for the Diophantine equation x^n + y^n = z^n where x, y, and z are integers has no solutions that are nonzero when n>2.
Background: Around 1637 Fermat claimed to have proven this theorem. He wrote in the margins of one of his books that when n>2 there were no solutions to the Diophantine equation. However, he did not prove his claim. 358 years later Andrew Wiles was able to successfully prove Fermat’s last theorem.
An example of a Proof of n=3: x^3 + y^3 = z^3
x^3 -1=(x-1)(x-t)(x-t^2) where t=e^2πi/3 Let x=x/y Can be rewritten as (x^3)/(y^3) – 1=(x/y -1)(x/y –t)(x/y –t^2) Now multiply both sides b y^3 and y become –y. Can be rewritten as z^3 = x^3 + y^3 = (x+y)(x+ty)(x+(t^2)y)
By looking at the prime factors of the left side of the above equation, it is impossible for it to equal z^3.
Andrew Wiles came up with an extensive proof for all “n” in 1994 and it was later published in 1995.
Resources: Rabinoff, J. (n.d.).Retrieved April 26, 2014, from http://people.math.gatech.edu/~jrabinoff6/mathcamp/lectures.pdf
http://www.mathsisfun.com/numbers/fundamental-theorem-arithmetic.html

