We all "understand" what the number 1 is. Right? How do you really explain what that is to a smart person that has never heard of it?
There is a mathematical way of doing it, through set theory. Discuss a little how that goes, how you define addition, and so on.
A Brief History on Natural Numbers
As most of us know, natural numbers are the numbers that we use to count (1, 2, 3, …). But, where did these numbers come from? Whether or not to include 0 has been debated throughout history. Zero was included to make the set more “complete.” This was because 0 represents an empty set. I said before that natural numbers are counting numbers. If you do not count any, you have 0 (an empty set). Whether or not 0 is included in the set of natural numbers depends on the field of mathematics, but most define the set starting at 1.
Defining Addition of Natural Numbers
There are many ways to define the addition of natural numbers: recursion, induction, set theory. However, for recursion and induction, we must look at the basic axiom of mathematics that a number, a, added to zero, is still a, or with the symbols:
n + 0 = n
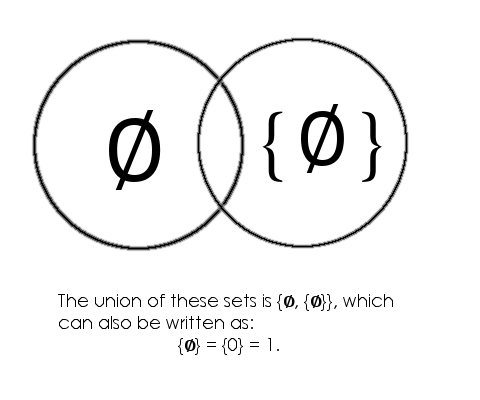
Set theory on the other hand defines “0” so that defining “1” becomes easier. Peano axioms, which states that n+0 =n, can be derived from set theory of natural numbers. These axioms are really helpful when it comes to defining the natural numbers as a whole, especially since a lot of mathematics is based off of this. The definition of “1” starts from the definition of zero, defined by John von Neumann, as an empty set (denoted as ∅), which can be written as 0 = ∅. What is interesting is that there is no formal proof/definition of "0" besides assuming that 0 = ∅, upon which the rest of this proof is based on and many other axioms are based on, including the previously mentioned Peano axioms.
By defining "1", we can then define the other numbers. Von Neumann also defines a function, s(n), where s is the successor function. The successor function is defined as s(n) = n+1. So if we use this idea of succession, we can define our successor function such that s(n) = n ∪ {n}. This successor function is especially useful in defining the natual numbers with respect to set theory because it allows us to cover the full set of natural numbers.
Proof Using Set Theory
Using Set Theory, we are able to construct a proof for defining the Natural numbers. The proof starts by defining zero in terms of sets and building from there.
We can let 0:=∅ which indicates zero is denoted as the empty set.
From there we use something called the Successor function. This function is a recursive function that is used to help define the natural numbers.
S(n) = n+1 Is the base of this function. Also “n” is denoted as any natural number. For example: S(1)=2 , S(2)=3 etc.
The easiest way to describe this is by saying that if you have nothing and and a collection of nothing, you still have a collection of nothing. Since we defined that nothing is the same as 0, we can state that we have a collection of 0, which we write as {0}.
0 = ∅
1 = s(0) = s(∅) = ∅∪ {∅} = {∅} = {0}
2 = s(1) = s({0}) = {0}∪Template:0 = {0, {0}} = {0,1}
So by this definition, via set theory, we can define "1" as a set containing only a single element, which we defined as 0.