What is a flow in a graph? What is a cut? How do they relate? Describe some ideas around these two concepts.
What is a flow in a graph?
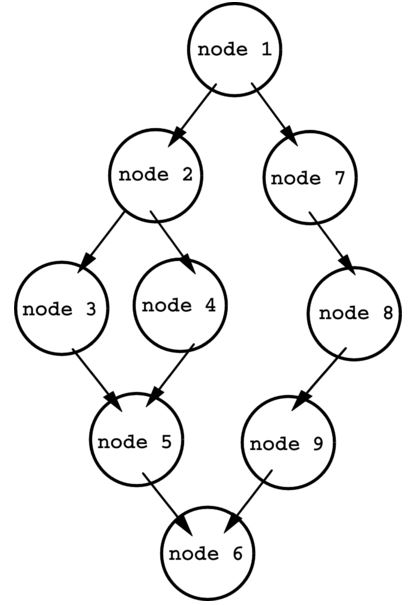
Useful in coding, flow graph is a visual representation of the various paths the code of a computer program can take. Flow in a graph is depicted using a series of arrows and nodes that display the route one can travel to each node. Each node represents a particular line of code in a program.
Here is a simple example of a flow graph:
- Node 1 is the initial line of code.
One of the primary purposes of creating a control flow graph is to discover whether there are parts of a computer program that are unnecessary. This can be achieved easily when looking at the control flow diagram. Any node that does not have an arrow connecting it to the rest of the nodes can be removed.
Another purpose a control flow graph serves is to help isolate problems such as infinite loops, where program execution does not move beyond a single node. Each arrow on the diagram shows what condition must be met to move to the node to which it points, so situations where that condition is never met can be spotted, because it causes the program to cycle back to the previous node over and over.
Finally, a control flow graph can help to create a program dependence graph. This type of graph shows what areas of a program are reliant on other parts. In computer science, this is used to establish an evaluation order to ensure that program code is executing in the correct sequence.
The visual nature of a control flow graph is one of the features that can make it potentially invaluable. Pieces of code that are never directly called or accessed will be fairly obvious, because there will either be no arrows linking it to the main program or the conditions will show that they can never be met to reach the code. There are computer programs that can automatically generate a control flow graph based on a series of source code files, further simplifying the process.
A control flow graph can be represented in any number of ways and, therefore, might appear differently depending on who has produced it. Some graphs use circles or squares exclusively to represent nodes while others use the same shapes as a standard flowchart . Although they are read in the exact same way, the method chosen is purely personal preference.
In graph theory, a cut is a partition of the vertices of a graph into two disjoint subsets that are joined by at least one edge. The cut-set of the cut is the set of edges whose end points are in different subsets of the partition. Edges are said to be crossing the cut if they are in its cut-set. (Many graph theorists use the term cut to refer to the edge set instead of the vertex partition.)
In an unweighted undirected graph, the size or weight of a cut is the number of edges crossing the cut. In a weighted graph, the same term is defined by the sum of the weights of the edges crossing the cut.
In a flow network, an s-t cut is a cut that requires the source and the sink to be in different subsets, and its cut-set only consists of edges going from the source's side to the sink's side. The capacity of an s-t cut is defined as the sum of capacity of each edge in the cut-set.
Definition
A cut is a partition of of a graph . An s-t cut of a network is a cut of such that and , where and are the source and the sink of respectively. The cut-set of a cut is the set . The size of a cut is the number of edges in the cut-set. If the edges are weighted, the value (or weight) of the cut is the sum of the weights. A bond is a cut-set that does not have any other cut-set as a proper subset.
Minimum Cut
A cut is minimum if the size of the cut is not larger than the size of any other cut. The illustration on the right shows a minimum cut: the size of this cut is 2, and there is no cut of size 1 because the graph is bridgeless.
The max-flow min-cut theorem proves that the maximum network flow and the sum of the cut-edge weights of any minimum cut that separates the source and the sink are equal. There are polynomial-time methods to solve the min-cut problem, notably the Edmonds-Karp algorithm.
Maximum cut
A cut is maximum if the size of the cut is not smaller than the size of any other cut. The illustration on the right shows a maximum cut: the size of the cut is equal to 5, and there is no cut of size |E| because the graph is not bipartite (there is an odd cycle).
In general, finding a maximum cut is computationally hard.[2] The max-cut problem is one of Karp's 21 NP-complete problems. The max-cut problem is also APX-hard, meaning that there is no polynomial-time approximation scheme for it unless P = NP. However, it can be approximated to within a constant approximation ratio using semidefinite programming.
Note that min-cut and max-cut are not dual problems in the linear programming sense, even though one gets from one problem to other by changing min to max in the objective function. The max-flow problem is the dual of the min-cut problem.
Cut space
The family of all cut sets of an undirected graph is known as the cut space of the graph. It forms a vector space over the two-element finite field of arithmetic modulo two, with the symmetric difference of two cut sets as the vector addition operation, and is the orthogonal complement of the cycle space.[8][9] If the edges of the graph are given positive weights, the minimum weight basis of the cut space can be described by a tree on the same vertex set as the graph, called the Gomory–Hu tree.[10] Each edge of this tree is associated with a bond in the original graph, and the minimum cut between two nodes s and t is the minimum weight bond among the ones associated with the path from s to t in the tree.
How Do They Relate?
In simple terms, we will get:
MAX FLOW = MIN CUT
Here is a proof from Eugene Lawler to explain this concept...
Let be a network (directed graph) with and being the source and the sink of respectively.
Consider the flow computed by Ford-Fulkerson algorithm. Define the residual graph in as follows: 1.: the set of vertices reachable from in . 2.: the set of remaining vertices.
Claim: value
where the capacity of an s-t cut is defined by .
Now, we know, for any subset of vertices, .
For value to be equal to , All outgoing edges from the cut must be fully saturated. All incoming edges to the cut must have zero flow.
To prove the above claim, let us assume that in , there exists an outgoing edge , ∈, ∈ such that it is not saturated.
i.e. This implies, that in , there exists a forward edge from to , which further implies that there
exists a path from to in , which is a contradiction. Hence, any outgoing edge is fully saturated.
Now, let us assume that in , there exists an incoming edge , ∈, ∈ such that it carries some non-zero flow. i.e. This implies, that in , there exists a backward edge from to , which further implies that there exists a path from to in , which is again a contradiction. Hence, any incoming edge must have zero flow.
Both of the above statements prove that the capacity of cut obtained in the above described manner is equal to the flow obtained in the network. Also, the flow was obtained by Ford-Fulkerson algorithm, so it is the max-flow of the network as well.
Also, since any flow in the network is always less than or equal to capacity of every
cut possible in a network, hence, the above described cut is also the min-cut which obtains the max-flow.
http://www.wisegeek.com/what-is-a-control-flow-graph.htm
http://en.wikipedia.org/wiki/Cut_(graph_theory)
Eugene Lawler (2001). "4.5. Combinatorial Implications of Max-Flow Min-Cut Theorem, 4.6. Linear Programming Interpretation of Max-Flow Min-Cut Theorem". Combinatorial Optimization: Networks and Matroids. Dover. pp. 117–120. ISBN 0-486-41453-1.